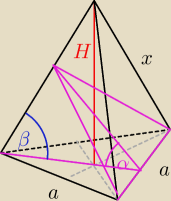
stereometria alicyjka: Przez krawędź podstawy prawidłowego ostroslupa trójkątnego poprowadzono płaszczyznę która jest nachylona do podstawy pod kątem α. Każda krawędź boczna ostroslupa tworzy z plaszczyzna podstawy kat β taki, ze 4sinβ=3sin(α+β). Oblicz stosunek pola powierzchni przekroju wyznaczonego przez te plaszczyzne do pola podstawy ostroslupa.

Jack: 4 sinβ = 3sin(α + β) to wiemy z tresci zadania

alicyjka: to juz wiem, obliczylam tez, ze sinβ=3/4=cosα

Godzio: Rozumiem, że to co wczoraj rozwiązałem Ci nie pasuje? Chyba, że dodajesz zadanie i o nim zapominasz?

Jack: β = 90 − α 4 sin(90 − α) = 3sin 90 4 cos α = 3

	3		hprzekroju
cos α =		=
	4		hpodstawy

	a√3
hpodstawy =
	2

zatem 4 h_przekroju = 3h_podstawy

	3hpodstawy		3a√3		3
hprzekroju =		=		=		a√3
	4		2*4		8

	1		3		3a2√3
Pole powierzchni przekroju =		* a *		a√3 =
	2		8		16

	a2√3
Pole podstawy =
	4

Zatem

Pprzekroju		3a2√3   16		3a2√3
	=		=		=
Ppodstawy		a2√3   4		4a2√3

	3
	4

taka jest odp?

Jack: aj, sory Godzio, nie widzialem

Godzio: Spoko to akurat nie Twoja wina ... Jak się wrzuca zadania to warto zajrzeć czy ktoś je zrobił czy nie.