zadanie 15(6p) CutieLana: wyznacz wszystkie wartości parametru a dla których równanie 3x⁵−5x³+a=0 ma dokładnie dwa pierwiastki. a=f(x)=−3x⁵+5x³ f'(x)=0 ⇔ 15x²(1−x)(1+x)=0 x=0 ⋁ x=1 ⋁ x=−1 f(−1)=−2 ⇒y_min f(1)=2 ⇒y_max i nie wiem co teraz zrobić...

ICSP: Masz wykres funkcja f(x). Po jakim przekształceniu otrzymasz wykres funkcji g(x) = f(x) + a ?

ICSP: Możesz również podejść inaczej : 3x⁵ − 5x³ = −a Za pomocą wykonanych przez ciebie obliczeń jesteś wstanie narysowac przybliżony wykres funkcji f(x) = 3x⁵ − 5x³. Potem wystarczy rysować proste poziome i sprawdzić kiedy taka prosta będzie miała tylko dwa punkty wspólne z wykresem.

CutieLana: Właśnie z narysowaniem tego wykresu mam problem. oprócz tego mam jeszcze lim x→∞ f(X)=+∞ i lim x→−∞ f(X)=−∞ jesteś w stanie pomóc z wykresem?

ICSP: Wyznaczyłeś/aś ekstrema. Wyznacz teraz przedziały monotoniczności poprzez rozwiazanie nierównośći : − f'(x) > 0 − f'(x) < 0 Mając ekstrema oraz przedziały monotonicznośći bez problemu narysujesz przybliżony wykres funkcji.

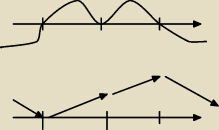
CutieLana: od lewej −1, 0 , 1 z tego mam monotoniczność, wcześniej też ekstrema, ale i tak nie wiem jak wykres

ICSP: Widzę, że odwrotnie zdefiniowałęś/aś funkcję niż ja. f(x) = −3x⁵ − 5x³ Ekstrema: − minimum w punkcie x = −1 równe f(−1) = −2 − maksimum w punkcie x = 1 równe f(1) = 2 Punkt przegięcia : − jeden w punkcie x = 0. Monotoniczność: f_↘ przedziałami : x ∊ (−∞ ; −1] ∪ [1 ; + ∞) f_↗ : x ∊ (−1 ; 1) Rysunek : Zaczynasz rysować od ćwiartki II. Funkcja maleje aż do punktu x = −1 w któym osiąga wartość −2. Potem zaczyna rosnąć przy czym w punkcie x = 0 rośnie bardzo łagodnie. Rośnie aż do punktu x = 1 w którym osiąga maksimum równe 2 i od tego punktu zaczyna maleć.

ICSP: f_↘ przedziałami : x ∊ (− ∞ ; −1] oraz , x ∊ [1 ; + ∞).

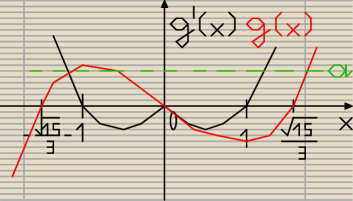
_xav: x₁ x₂, ∊ R {x₃, ..., x_∞} ∊ ∅ x₁ ≠ x₂ f(x) = 3x⁵ − 5x³ + a = 0 g(x) = 3x⁵ − 5x³ = −a

	5
g(x) = 3x3(x2−		)
	3

	√15		√15
g(x) = 3x3(x−		)(x+		)
	3		3

g'(x) = 15x⁴ − 15x² g'(x) = 15x²(x²−1) g'(x) = 15x²(x−1)(x+1) −a = g(−1) = −3 + 5 = 2 −a = g(1) = 3 − 5 = −2 −a ∊ {−2, 2} a ∊ {−2, 2}