Rozpatrujemy odcinki równoległe do osi o y których jeden koniec leży na wykresi bolek amator: Rozpatrujemy odcinki równoległe do osi o y których jeden koniec leży na wykresie funkcji kwadratowej f określonej wzorem y=x² a drugi koniec leży na wykresie funkcji G określonej wzorem g(x)=√x dla x≥0 Oblicz długość najkrótszej takiego odcinka. Dotarłem do momentu w którym r−nie z którego mamy znaleźć minimalną wartośćf(x)= |x² + 2 + √x| jak pokonać rachunki ?

bolek amator: (Edit) *najkrótszą długość tego odcinka

g: Najkrótszy odcinek ma długość zero, od punktu (1,1) do punktu (1,1). Ten punkt, jak również punkt (0,0) leżą na obu wykresach. Chyba coś jest nie tak ze sformułowaniem zadania.

Mila: Też takie mam wrażenie, że to bez sensu.

bolek amator: Przepraszam oczywiście funkcja kwardatowa miała mieć wzór x² +2, my bad

Janek191: x² + 2 to nie jest funkcja kwadratowa Powinno być, np. y = x² + 2 lub f(x) = x² + 2

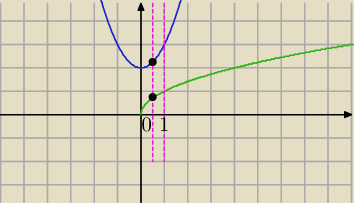
Mila: A=(x,√x) B=(x,x²+2) x>0 |AB|=√(x²+2−√x)²=|x²−√x+2|=x²−√x+2 d(x)=x²−√x+2

	1
d'(x)=2x−
	2√x

	1
2x−		=0
	2√x

	1
2x=		⇔
	2√x

4x√x=1

	1
√x3=		/2
	4

	1
x3=
	16

	1
x=
	23√2

	1
d'(x)>0⇔2x−		>0 i x>0
	2√x

	1
2x>		/* 2√x
	2√x

4x√x>1

	1
x>
	23√2

	1
d'(x)<0 dla x∊(0,		)⇔
	23√2

	1
dla x=		funkcja d(x) osiąga minimum
	23√2

=================================