Geometria analityczna Ziqu: Punkty A=(−3,0), B=(1,8), C(−1,9) są wierzchołkami trapezu ABCD, którego ramię AD zawiera się w prostej o równaniu y= −x − 3 . Wyznacz współczędne wierzchołka D. Nie mam pomysłu na to zadanie

5-latek : A ja mam pomysl na początek Zrobic rysunek do zadania i zobaczyć co wyjdzie

Ziqu: Zrobione. I dalej nie mam pomysłu.

5-latek : no to narysuj tutaj

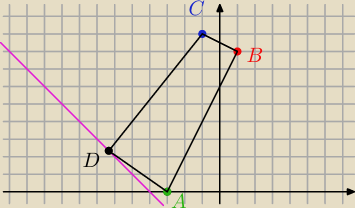
Jack: rysunek pogladowy... jesli to ma byc trapez to prosta zawierajaca punkty B i C musi byc rownolegla do prostej na ktorej jest punkt D czyli −x − 3 wiec proponuje tak 1. Wyznaczyc wspolczynnik kierunkowy prostej CB 2. podstawic ten wspolczynnik oraz punkt A i znalezc ta prosta (przechodzaca przez A) 3. znalezc przeciecie sie prostej y = −x − 3 oraz prostej z punktu 2.

Ziqu: współczynnik prostej CB = − 1/2 , a współczynik prostej DA = −1 (wnioskuję po równaniu prostej) więc one nie są równoległe ( ?)

Ziqu: Ale ok. wyznaczam prostą DA 0= − ¹₂ x −3 + b 0=³₂ + b b= −³₂ y=−¹₂x−³₂

Ziqu: y= −x − 3 y= −¹₂x − ³₂ −x − 3= −¹₂x − ³₂ x=−3 y=0 I to jest źle

5-latek : Kombinujesz dobrze Tylko tak : nie równanie prostej DA tylko równanie prostej rownoleglej do prostej CB i przechodzącej przez punkt A ( bo podstawy w trapezie sa rownolegle

	1
Wspolczynnik kierunkowy a prostej CB a=−
	2

Wobec tego równanie tej prostej rownoleglej będzie takie y=ax+b

	1		3
0=−		*(−3)+b to b=−
	2		2

Rownanie tej prostej będzie takie jak napisals w poscie 17:59 Żeby wyznaczyć wsplrzedne punktu D musimy wyznaczyć punkt przecięcia się tej prostej

	1		3
y=−		x−		z prosta y=−x−3
	2		2

	1		3
−		x−		= −x−3
	2		2

	1		3
−		x+x=−3+
	2		2

1		3
	x=−
2		2

x= policz Potem wstaw wyliczony x do równania np. prostej y=−x−3 i wylicz y

5-latek : Możesz również wstawić wyliczony x do równania y=−0,5x−1,5 i wyliczyć y (powinno wyjść to samo

Ziqu: No i znowu wychodzi mi x=3 a y = 0. A w odp jest inaczej

5-latek : T jest tak jak się nie potrafi liczyc Jakim cudem z podzielenia liczby ujemnej i dodatniej wyjdzie liczba dodatnia ? Poza tym jeśli wyszlo CI x=3 to patrząc na rysunek już widać ze cos jest nie tak

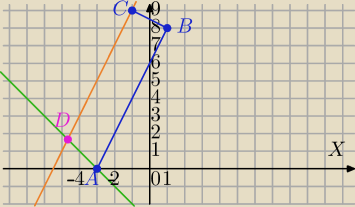
Mila: Punkty A=(−3,0), B=(1,8), C(−1,9) AD: y=−x−3 AB: y=ax+b −3a+b=0 a+b=8 −−−−−−−−−− odejmuję stronami: −4a=−8 a=2 y=2x+b Prosta DC: y=2x+b i C∊prostej⇔9=2*(−1)+b⇔b=11 y=2x+11 D − punkt przecięcia prostych: y=2x+11 i y=−x−3 2x+11=−x−3

	14
3x=−14⇔x=−
	3

	14		5
y=		−3=
	3		3

	14		5
D=(−		,		)
	3		3

AB||DC

5-latek : Dobry wieczor Milu Pozdrawiam sprawdziłem ze tez dla 0,5x=−1,5 wyjdzie x=−3 a to tez jest nieprawda z rysunku wiec gdzie jest blad u mnie w liczeniu ?

5-latek :

	9−8		1
wspolczynnik prostej BC to		= −
	−1−1		2

5-latek : Już wiem w ogole złe myslenie Punkty A i D maja lezec na jednej prostej

Mila: Witam świątecznie. właśnie , przecież AD nie może być równoległe do BC.

5-latek : Wiec nalezalo poprawadzic prosta rownolegla do AB i przechodzaca przez punkt C Wtedy wyznaczyć punkt D .

Mila: Zgadza się.

5-latek : Dobrze