Objętość walca kam: Rozpatrujemy wszystkie walce, których przekrojem osiowym jest prostokąt, w którym suma długości przekątnej i jednego boku jest równa 10. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz objętość tego walca. Zrobiłem 2 przypadki w jednym wyszło mi że V max gdy h=2,5 i V=31,25. Czy jest możliwość, że w drugim przypadku r=2,5 i wtedy wysokosc mi się wyzeruje? Czyli de facto nie będzie drugiej objętości?

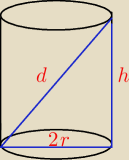
Jack: jak rozumiem raz wziales d+h = 10 a drugi raz 2r + d = 10 Zobaczmy wiec... 1) z pitagorasa d² = h² + 4r² d+h = 10 −−>> d = 10 − h (10−h)² = h² + 4r² 100 − 20h +h² = h² + 4r² 4r² = 100 − 20h r² = 25 − 5h Pomijam zalozenia i inne takie... V = π r² h V = π * h (25 − 5h) = π(−5h² + 25h) zatem V '(h) = π (−10h + 25) −10h + 25 = 0 h = 2,5

	5√2
r =
	2

(znowu pominalem zalozenia, przedzialy monot. itd) Teraz drugi przypadek d² = h² + 4r² 2r + d = 10 −−−>> d = 10 − 2r 100 − 40r + 4r² = h² + 4r² h² = 100 − 40r V = π r² * √100 − 40r =π √r⁴(100−40r) = π√−40r⁵ + 100r⁴ niech f(r) = −40r⁵ + 100r⁴ (osiaga ekstrema w tym samym miejscu co V, tylko wartosc inna, ale ten sam argument) f ' (r) = − 200r⁴ + 400r³ −200r⁴ + 400r³ = 0 −r⁴ + 2r³ = 0 r³(−r + 2) = 0 r³ = 0 lub r = 2 dla r = 2 mamy Vmax h = √100 − 40*2 = √20 = 2√5 czyli dla 1. h = 2,5

	5√2
r =
	2

V = π(−5h² + 25h) = π (−5 * 6,25 + 25 * 2,5) = 31,25π dla 2. r = 2 h = 2√5 V = π√−40r⁵ + 100r⁴ = π√−40*(32) + 100(16) = π * √320 ≈ 17,89π ewidentnie widac ze dla pierwszego jest wieksza...

kam: Dzięki, teraz patrze, że zapomniałem pochodnej policzyć w 2 przypadku..