PIlne Adrian: Zadania z geometrii Witam, prosiłbym o rozwiązanie tych zadań 1. W równoległoboku ABCD z wierzchołka kąta rozwartego poprowadzono dwie wysokości DP i DQ (P∊AB , Q∊BC ) a) udowodnij, że na czworokąt DPBQ można opisać okrąg b) oblicz promień okręgu opisanego na czworokącie DPBQ, jeśli podstawy równoległoboku mają długość 15 i 33, a krótsza wysokość DP = 12. 2. W trójkącie prostokątnym ABCD (AB ll CD , AD ⊥ AB ) o krótszej podstawie DC mającej długość równą 3 wpisano okrąg o środku w punkcie O i r =2 . a) udowodnij, że trójkąt BOC jest prostokątny b)oblicz stosunek r/R promieniu okręgu wpisanego w trójkąt BOC do promienia okręgu opisanego na tym trójkącie 3. W trapezoidzie ABCD połączono środki boków, tworząc czworokąt PQRS. a) udowodni, że PQRS jest równoległobokiem b) oblicz obwód PQRS, kąt a =120 stopni , kąt D = 60 stopni , AB = 5 , AD = 4 , DC=7 4. Romb A1B1C1D1 jest obrazem rombu ABCD w podobieństwie o pewnej danej skali k (k>0). Kąt ostry rombu A1B1C1D1 = 60 stopni, suma długości przekątnych rombu ABCD = d. Wyznacz długość boku rombu A1B1C1D1 .

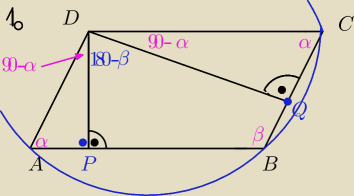
Jack: mozna opisac jesli α + α = 180 α = 90 oraz β + 90 − α + 90 − α + 180 − β = 180 360 − 2α = 180 2α = 180 α = 90 wychodzi na to ze to jest kwadrat... aczkolwiek nic chyba nie wykazalem ;x

Jack: albo prostokat...