metis
Metis: 2 proste zadanka
 Janek
Janek ma d litrów solanki o stężeniu d% . Ile litrów soli musi dodać aby solanka miała
steżenie 3d%.
Metodą kubełkową?
| | x−0,5 | | 3x+a | |
2) Wzór g(x)= |
| można zapisać w postaci |
| . Iloczyn abc jest równy? |
| | 2x+1 | | bx+c | |
Dla mnie b=2 , c=1
| | a | |
W liczniku 3(x+ |
| ) , zatem |
| | 3 | |
Zatem a=−4,5
−4,5 *1*3 = −9
Odp.:−27
26 mar 15:28
Metis: Coś przekombinowałem z licznikiem w tym 2 .
26 mar 15:32
26 mar 15:32
Metis: Siemka
Benny 
Jak to zapisać

26 mar 15:34
26 mar 15:36
Eta:
a= −1,5 , b=6 , c= 3
abc = −27
26 mar 15:36
Benny: Cześć

26 mar 15:36
Eta:
.......................

26 mar 15:38
Metis: Okey chyba mam

| | 1 | | x−0,5 | | x−0,5 | |
Zatem |
| * |
| = |
| |
| | 3 | | 2x+1 | | 6x+3 | |
| | a | |
−0,5= |
| wtedy gdy a=−1,5 |
| | 3 | |
26 mar 15:38
Metis: A z tym 1) pomożecie ?

26 mar 15:40
Eta:
Kubełkami

26 mar 15:41
Janek191:
| d*d100 + x | | 3 d | |
| = |
| |
| d + x | | 100 | |
d
2 + 100 x = 3 d*(d + x)
d
2 + 100 x =3 d
2 + 3 d x
100 x −3 d x = 2 d
2
( 100 − 3 d) x =2 d
2
26 mar 15:42
Kacper:
Kubełki potrzebne na poniedziałek

26 mar 15:46
Janek191:

26 mar 15:46
Metis: Dzięki

26 mar 15:50
Eta:
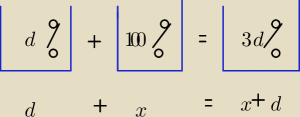
| | 2d2 | | 100 | |
d2+100x=3dx+3d2 ⇒ (100−3d)x=2d2 ⇒ x= |
| , d∊(0, |
| ) |
| | 100−3d | | 3 | |
26 mar 15:53
Eta:
"kubełki" załatwiają problem w jednej linijce...........

26 mar 15:54
Metis: 

26 mar 16:04
26 mar 16:06
Metis: Wyznacz współczynnik stojący przy x
3 w wyrażeniu (x
2+x+1)
13
Kombinować drzewkiem Pascala ?

26 mar 16:06
Janek191:
| | √x + x | | 1 | | √3 | |
lim |
| = |
| = |
| |
| | √3 x − √3 x | | √3 | | 3 | |
x→0
+
26 mar 16:25
Godzio:
| | | |
(x2 + x + 1)13 = ∑i=013 | (x2)i * (x + 1)13 − i = |
| | |
| | | | | |
= ∑i=013 | (x2)i * ∑k=013 − i | xk = |
| | | |
Poszczególne wyrazy mają postać:
2i + k = 3 ⇒
| | | | | |
1. k = 3 oraz i = 0 ⇒ | * | * x3 = 22 * 13 * x3 |
| | | |
| | | | | |
2. k = 1 oraz i = 1 ⇒ | * | * x3 = 12 * 13 * x3 |
| | | |
W sumie: 34 * 13 = 442
26 mar 16:31
Metis: O kurcze , to na pewno poziom liceum ?

Możesz mi to wytłumaczyć
Godzio ?
26 mar 16:32
Godzio:
Wiadomo co oznacza symbol ∑?
26 mar 16:33
Metis: Sumę

26 mar 16:34
Godzio:
No dobra,
Dobra to podam najpierw przykład, żeby była pewność, że wiadomo o czym mówię.
a
1 + a
2 + a
3 + ... + a
n = ∑
i = 1na
i
W dolnym indeksie zapisuję odkąd zaczynam, i = 1, w górnym zapisuje na czym kończę.
Inne przykłady:
1 + 2 + 3 + 4 + ... + n = ∑
i=1n i
1 + x + x
2 + x
3 + .. + x
n = ∑
i = 0n x
i
Wzór na dwumian Newtona:
| | | |
(a + b)n = ∑i=0n | an − ibi bo |
| | |
| | | | | | | |
(a + b)n = | anb0 + | an − 1b1 + | an − 2b2 + ... + |
| | | | |
U nas traktuje a = x + 1, b = x
2 oraz n = 13
| | | |
∑i=013 | (x2)i * (x + 1)13 − i |
| | |
I teraz z tego samego wzoru rozpisuje (x + 1)
13 − i
| | | |
(x + 1)13 − i = ∑k = 013 − i | xk * 113 − i − k = |
| | |
Wklepuje do początkowej sumy:
| | | | | |
∑i=013 | (x2)i * ∑k = 013 − i | xk |
| | | |
Początek nie zależy od 'k' więc mogę to włączyć do wewnętrznej sumy:
| | | | | |
∑i=013∑k = 013 − i | (x2)i | xk |
| | | |
Po przemnożeniu:
| | | | |
∑i=013∑k = 013 − i | x2i + k |
| | |
26 mar 16:40
Benny: Takie zadanka są w w Krysickim na początku jak dobrze pamiętam.
26 mar 16:43
Metis: Przeanalizuję dokładnie i będę pytał w razie wątpliwości

Dzięki
Godzio za czas , nie sądziłem że to tak złożone zadanie.
26 mar 16:44
Metis: I w Aksjomacie

26 mar 16:44
Godzio:
Jak się jest obytym w temacie to nie takie trudne

Na początek próbuj zadania z dwoma czynnikami typu:
(x +
√x)
15
Jak jest współczynnik przy x
5 
26 mar 16:53
Metis: Zajmę się tym za chwilę , jak napiszę to wrzucę

26 mar 17:03
bezendu:
(x+
√x)
15
n 15
| | | | | |
(a+b)n=∑ | a15−ibi=∑ | x15−i√xi |
| | | |
i=0 i=0
=x
15+15x
14√x+105x
13(
√x)
2+455x
12(
√x)
3+1365x
11(
√x)
4+3003x
10(
√x)
5
+5005x
9(
√x)
6+6435x
8(
√x)
7+6435x
7(
√x)
8+5005x
6(
√x)
9+3003x
5(
√x)
10
+1365x
4(
√x)
11+455x
3(
√x)
12+105x
2(
√x)
13+15x(
√x)
14+(
√x)
15
=x
15+15x
14√x+105x
13(
√x)
2+455x
12(
√x)
1365x
11(
√x)
4+3003x
10(
√x)
5
+5005x
9(
√x)
6+6435x
8(
√x)
7+6435x
7(
√x)
+5005x
6(
√x)
9+3003x
5(
√x)
10
+1365x
4(
√x)
11+455x
3(
√x)
12+105x
2(
√x)
13+15x(
√x)
14+(
√x)
15
=x
15+15x
29/2+105x
14+455x
27/2+1365x
13+3003x
25/2+5005x
12+6435x
23/2
+6435x
11+5005x
21/2+3003x
10+1365x
19/2+455x
9+105x
17/2+15x
8+x
15/2
Jedno z moich zadań na początku studiów
 =================================
=================================
26 mar 17:55
bezendu:
w dwóch miejscach widzę potęgi sprawiły psikusa

4 linijka 1365x
11(
√x)
4+3003x
10(
√x)
5
26 mar 18:05
Godzio:
Że też Ci się chciało to pisać

26 mar 21:38
bezendu:
Przerwa świąteczna to nudy, ale całki powierzchniowe sobie powtórzę

26 mar 22:00
Kacper:
No i ciekawe, który maturzysta to będzie liczył

Trzeba sposobem, a nie na ...

27 mar 08:18
5-latek : Żaden nie policzy bo nie musi
Zadanie pewnie jest ze starego aksjomatu
27 mar 08:34
Metis: 5−latku to moje z najnowszego

27 mar 14:06
 Janek ma d litrów solanki o stężeniu d% . Ile litrów soli musi dodać aby solanka miała
steżenie 3d%.
Metodą kubełkową?
Janek ma d litrów solanki o stężeniu d% . Ile litrów soli musi dodać aby solanka miała
steżenie 3d%.
Metodą kubełkową?
 Jak to zapisać
Jak to zapisać 








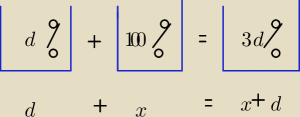




 Możesz mi to wytłumaczyć Godzio ?
Możesz mi to wytłumaczyć Godzio ?

 Dzięki Godzio za czas , nie sądziłem że to tak złożone zadanie.
Dzięki Godzio za czas , nie sądziłem że to tak złożone zadanie.

 Na początek próbuj zadania z dwoma czynnikami typu:
(x + √x)15
Jak jest współczynnik przy x5
Na początek próbuj zadania z dwoma czynnikami typu:
(x + √x)15
Jak jest współczynnik przy x5 

 =================================
=================================
 4 linijka 1365x11(√x)4+3003x10(√x)5
4 linijka 1365x11(√x)4+3003x10(√x)5


 Trzeba sposobem, a nie na ...
Trzeba sposobem, a nie na ... 
