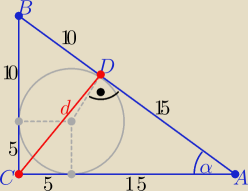
matura 2016 hegel: W trójkąt prostokątny o przyprostokatnych 15 i 20 wpisano okrąg. Oblicz długośćg odcinka łączącego wierzchołek kąta prostego tego trójkąta z punktem wspólnym okręgu i przeciwprostokatnej.

Eta:

	a+b−c
a=20, b=15 ,c=25 r=		=...=5 i |AD|=15 , |BD|=10
	2

	20		4
cosα=		=
	25		5

z tw. kosinusów w ΔCBD d²=20²+15²−2*20*15*cosα d²= 625−480 ⇒ d=√145

Eta: Poprawiam chochlika ..... z tw. kosinusów w Δ CAD

zzzz: rozwiazalam zadanie innym sposobem ale otrzymałam inny wyniki chciałabym wiedzieć czy jestem w stanie go użyć, skąd błędny wynik itp bo uważam że sposób ten jest szybszy oczywiście jeżeli jest poprawny zaczęłam od tw pitagorasa stąd dowiedziałam się że przeciwprostokątna ma 25 a później wykorzystałam wzór dostępny w kartach odnośnie wysokości w trójkącie prostokątnym hc =ab/c także wynik końcowy równy jest 12

Jolanta: Wyszłaś z założenia ,że odcinek którego szukasz jest wysokością A tak nie jest

zzzz: dziekuje bardzo, pominęłam ten element juz wszystko jasne, jeszcze raz dziękuję