trygonometria Azul: Funkcja trygonometryczna wyznacz zbiór wartości f−ji f(x)=4sinx+cos2x 4sinx+cos²x−sin²x 4sinx+1−sin²x−sin²x −2sin²x+4sinx+1 sinx=t, t∊<−1;1> f(t)=−2t²+4t+1 i tu się trochę pogubiłam policzyłam p=1 q=3 potem zobaczyłam że q jest chyba niepotrzebne ale ogólnie to za bardzo nie wiem co robić dalej próbowałam policzyć f(t) dla −1 i 1 i wyszło mi 3 i −1 ktoś może mi pomóc co dalej?

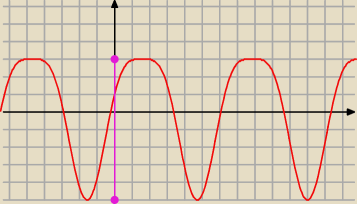
Janek191: f(x) = − 2 sin² x +4 sin x + 1 , − 1≤ sin x ≤ 1 f(−1) = − 2 − 4*1 + 1 = − 5 f( 1) = − 2 + 4 + 1 = 3 ZW = < − 5 , 3 > ============

Azul: o Dziękuje Janek191 czyli niepotrzebnie zamieniałam sinx na t

Janek191: Dobrze zrobiłaś, bo mój zapis nie jest do końca poprawny.

Azul: racja teraz wychodzi mi dobrze tak jak robiłam 5 razy przeliczałam i 5 razy gubiłam − xD

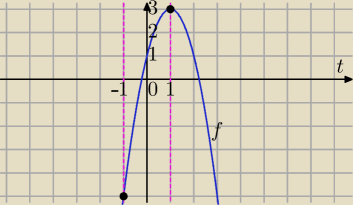
Mila: f(x)=4sinx+cos2x⇔ f(x)=−2sin²x+4sinx+1 sinx=t i |t|≤1 f(t)=−2t²+4t+1 i t∊<−1,1> parabola skierowana w dół

	−4
tw=		=1∊<−1,1>⇔
	−4

największa wartość f(t) dla t=1 f(1)=−2+4+1=3 Najmniejsza dla x=−1 f(−1)=−2*(−1)²−4+1=−5 Zw_f=<−5,3>

Azul: zadanie mam już rozwiązane ale Twoja odp pomogła mi w drugim zadanku