zadanie Metis: Maksymalne n∊N , dla którego 2ⁿ jest dzielnikiem 20! jest równe Jakiś pomysł ?

Benny: Czy odp to 2¹⁸?

Benny: Sprawdź ile jest dwójek w rozkładzie. Może robiłeś kiedyś takie zadanie, gdzie trzeba było policzyć ile 100! bodajże ma zer?

Kacper: Odpowiedź, to 18.

Metis: Benny podobne zadanie trafiło mi się na II etapie AGH'u, nie wiedziałem jak zrobić.

Metis: http://prntscr.com/ajwpg2

Kacper: 2 → 1 dwójka 4 → 2 dwójki 6 → 1 dwójka 8 → 3 dwójki 10 → 1 dwójka 12 → 2 dwójki 14 → 1 dwójka 16 → 4 dwójki 18 → 1 dwójka 20 → 2 dwójki ============= łącznie 18 dwójek. Sposób "na piechotę".

Metis: Bierzemy tylko parzyste bo w rozkładzie liczb nieparzystej 2 nie będzie?

Kacper: Zadanie ze zdjęcia. 2016<5⁵, zatem Liczba 2016! ma w zapisie dziesiętnym

	2016		2016		2016		2016
[		]+[		]+[		]+[		]=403+80+16+3=502
	5		52		53		54

zera. Zatem jest podzielna przez 10⁵⁰², czyli k jest równe 502.

Metis: Na zadanie ze zdjęcia mam gdzieś jeszcze inne rozwiązanie, zapisane przez mojego profesora, muszę poszukać

Metis: Dzięki Kacper Idąc tym "tropem", ile zer ma 100! . Czyli 100<5³

100		100
	+		= 20+4=24 zera?
5		25

Metis: Oczywiście 100=10²

Kacper:

Metis: Super

Saizou : Cześć Wam i chwała Kacper jesteś może na gg ?

Kacper: Tak, tylko nie bij Zapomniałem

Metis: Siemka Saizou

Saizou : Kacper nie mam takiego zamiaru Siemasz Metis

Saizou : 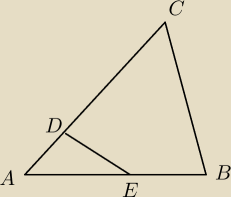Zadanko na poziomie podstawówki W trójkącie ABC punkt E jest środkiem boku AB, a odcinek AC jest 3 razy dłuższy od odcinak AD. Pole trójkąta ABC jest równe 30. Oblicz pole trójkąta AED

Metis: Nie brakuje niczego?

Desperat: Paed=4*30−α= 14

Benny: Odp. to 5?

Saizou : tak, a rozwiązanie

Metis: Ze wzoru Herona? i zabawa z obwodem?

Benny:

	1
Zastosuj wzór P=		absinα
	2

Saizou : ojojoj.... na poziomie podstawówki

Metis: Od razu odrzuciłem trygonometrię brak związków kątowych

Saizou :

	1
proponuje tylko wzór "P=		ah"
	2

Metis: Mam...

Metis: Albo nie Tam nie ma kąta prostego. Chciałem skorzystać z h=√z*z₁ , gdzie z i z₁ to odcinki na które dzieli odcinek spodek wysokości

Saizou : ew. zgodzę się na podobieństwo

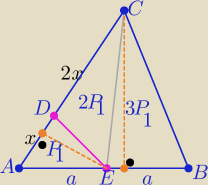
E: 6P₁=30 ⇒ P₁=P(AED)=5

prosta:

P1		0,5 *x*a*sinα
	=
P		0,5*3x*2a*sinα

P1		1
	=
30		6

P₁=5

Eta:

Saizou : brawo E

E:

Metis:

	33		5
Liczby naturalne m. n spełniają warunek		=m+		, suma równa m+n
	7		n

Nie potrafię przekształcić by uzyskać tę sumę

Mila: Obliczymy ile " dwójek " będzie w rozkładzie 20! na czynniki pierwsze. Liczymy tak:

	20
[		]=10
	2

znak [..] oznacza całkowitą część liczby To nie wszystkie dwójki, liczba 4=2*2 ma dwie dwójki w rozkładzie na czynniki pierwsze, jedną dwójkę już policzyliśmy.

	20
[		]=5
	4

Liczba 8=2*2*2 ma 3 dwójki w rozkładzie na czynniki pierwsze, dwie już policzyliśmy

	20
[		]=2
	8

dalej:

	20
[		]=1
	16

	20
[		]=0
	32

Liczba 20! ma w rozkładzie na czynniki pierwsze : 10+5+2+1=18 dwójek Największy dzielnik 2ⁿ to 2¹⁸ =====

5-latek :

Mila: 21:17 to cała treść zadania?

Metis: Dobry wieczór Milu ...,zatem suma m+n jest równa : 8 9 10 11 Nie wiem jak to policzyć

Mila: Trzeba rozwiązać równanie w zbiorze N

33		5
	=m+
7		n

Wyznaczymy n

33		5
	−m=
7		n

33−7m		5
	=		⇔
7		n

n		7
	=
5		33−7m

	35
n=		prawa strona może być liczbą naturalną dla pewnego dzielnika liczby 35
	33−7m

	32
33−7m=1⇔32=7m, m=		∉N
	7

33−7m=5⇔28=7m⇔m=4 wtedy n=7 ⇔m+n=11 i koniec, bo to test jednokrotnego wyboru. W zadaniu otwartym trzeba sprawdzić jeszcze dwa warunki.

Mila: II sposób Po kolei podstawiasz m+n=8 m=8−n i równanie w zbiorze N

33		5
	=8−n+		ale to chyba będzie więcej liczenia,
7		n

złośliwie podali na końcu prawidłową odpowiedź. Spróbuj w sposobie z 22:07 wyznaczyć m ale chyba gorzej będzie.

Metis: Dziękuję pięknie Milu

Mila:

Mila: