parametr glax: wyznacz liczbę rozwiązań równania |x²−1|=3−m² ze względu na wartość parametru m(m∊R).

Metis: Graficznie

glax: noooo tak

glax: f(x)=|x²−1| g(x)=3−m² f₁(x)=x² f₂(x)=x²−1 f₃(x)=|x²−1| o to chodzi?

glax: up

Metis: Rysujesz f(x) , prostą y=... I badasz położenie prostej y i liczbę rozwiązań. Otrzymane wyniki podstawiasz do twojej g(x) i otrzymujesz wartości parametru m.

olekturbo: Narysuj f(x) = |x²−1|−3 i sprawdź dla jakich wartości przecina ją g(x) = −m²

glax: jeszcze jaki wektor?

zef: Rysujesz lewa stronę równania i przyjmujesz że k=3−m² Badasz to dla prostej k ile jest punktów przecięcia i później podstawiasz za k=3−m²

Metis: Dokładnie to napisałem Jednak z tą równością uważałbym − np. poniżej y=0 rozwiązań brak

glax: y=x² , u=[0,−1] →→y=x²−1

Metis: Rysuj f(x)=|x²−1|

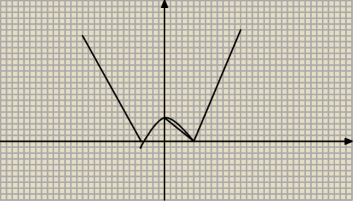
glax: genialnie mi wyszło^^

Metis: http://prnt.sc/ajtqvs

glax: gdy: k< brak rozwiązań k=0 ∧ k>1 dwa rozwiązania k=1 trzy rozwiązania k>0 ∧ k<1 cztery rozwiązania

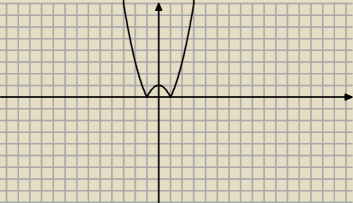
zef: Metis na tej stronie możesz rysować funkcję podając jej równanie

glax: Metis właśnie o to mi chodziło

glax: faktycznie a ja się tak męczyłem z tym wykresem

Metis: Jeśli y<0 brak rozwiązań Jeśli y=0 dwa rozwiązania Jeśli 0<y<1 cztery rozwiązania Jeśli y=1 trzy rozwiązania Jeśli y>1 dwa rozwiązania , zatem Brak rozwiązań: 3−m²<0 ⇔ m∊(−∞, −√3)U{√3 , +∞) Możemy sprawdzić np . dla 2 |x²−1|=3−4 = |x²−1|=−1 − brak rozwiązań. Dalej analogicznie.

glax: dziękuje wszystkim za pomoc