geometria jacek: W trójkąt równoramienny ABC o podstawie długości |AB|=14 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek A z punktem wspólnym okręgu i ramienia BC.

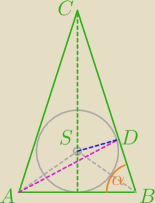
===: r=?

	3
∡ASD=180−α+90−α/2=270−		α
	2

|AS|=? |SD|=r |AD|= z twierdzenia cosinusów ale pewnie jest prostszy sposób

jacek: a czy moge zrobic tak ze policze cosinus kąta alfa − cosx=7/25 i majac dlugosc podstawy czyli 14 i długosc odcinka |DB| policze z tw cosinusow odcinek |AD| Tylko ile wynosi odcinek |DB|?

===: |DB|=7 (pół podstawy)

===: i masz łatwiejszy sposób Z podstawy i pola ....wyliczysz h trójkąta ... potem α ... a z tego już |AD|