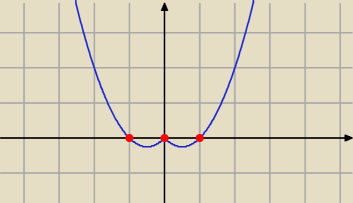
nie kumam ehem: ile ma miejsc zerowych funkcja f(x)=x² − |x| ?

Eta: 3

Eta:

zef: x²−x=0 dla x≥0 x(x−1)=0 x=0 lub x=1 Oba należą do Df. 2 przypadek gdy x<0 x²+x=0 x(x+1)=0 x=0 x=−1 Oba należą do Df Po zsumowaniu mamy 3 miejsca zerowe: −1,0,1

Metis: Algebraicznie: f(x)=x²−|x| f(x)=0 ⇔ x²−|x| =0 1) Jeśli x≥0 x²−x=0 x(x−1)=0 x=0 v x=1 {0, 1} ∊ <0, +∞) 2) Jeśli x<0 x²+x=0 x(x+1)=0 x=0 v x+1=0 x=0 v x=−1 x=0 ~∊ (−∞, 0) x=−1 v x=0 v x=1 3 rozwiązania.

Metis: zef w drugim przypadku x<0 , 0 nie należy.

zef: W 2 przypadku oczywiście do Df należy tylko −1, taki mały błąd mi się wkradł

zef:

Saizou : x²−|x|=0 x²=|x| /² x⁴=x² x²(x−1)(x+1)=0 i bez przypadków

Eta: