Funkcje ernest: 7. Dla poniższych parabol: a) y = 3x2, b) y = − x2 + 2x – 15, c) y = x2 – 2x + 1, d) y = 2x2 + x + 3. − Oblicz (jeżeli istnieją) miejsca zerowe oraz współrzędne wierzchołka, − Napisz równanie prostej, która jest ich osią symetrii, − Podaj zbiór wartości funkcji − Napisz równanie funkcji w postaci iloczynowej i kanonicznej − Narysuj wykres danych funkcji.

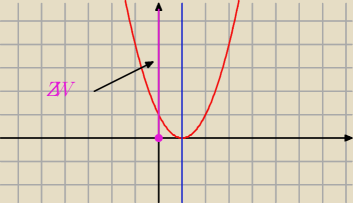
Janek191: Np. c) y = x² −2 x + 1 y = x² −2 x + 1 = ( x − 1)² = 0 ⇔ x = 1 − miejsce zerowe

	− b		2
p =		=		= 1
	2a		2

x = 1 − równanie osi symetrii q = f(p) = f(1) = 0 ZW = < q , +∞ ) = < 0, +∞) − zbiór wartości y = ( x − 1)² = ( x −1)*( x −1) − postać iloczynowa y = a*( x − p)² + q = ( x − 1)² − postać kanoniczna bo a = 1 i q = 0 wykres : a = 1 > 0 W = ( p, q ) = (1 , 0)

ernest: Dzięki bardzo