Nierówność trygonometryczna. jeheeze: Witam, mam do rozwiązania taką oto nierówność: sin3x−sinx<sin2x Doszedłem do takiej formy iloczynowej: sinx(2cosx+1)(cosx−1)<0 Mógłby ktoś mi pomóc co dalej?

jeheeze: Odświeżam, wciąż nic nie wykombinowałem

Mila: sin3x−sinx<sin2x⇔

	3x+x		3x−x
2*cos		*sin		<sin(2x)⇔
	2		2

2*cos(2x)*sinx<2 sinx *cosx cos(2x)*sinx− sinx *cosx<0 sinx*(cos(2x)−cosx)<0 (sinx>0 i cos(2x)−cosx<0) lub (sinx<0 i cos(2x)−cosx>0) Spróbuj dalej sam, teraz już nie mam czasu, będę po 20, jeżeli nikt nie pomoże, to napisze.

jeheeze:

	π
Z pierwszego przypadku wyszło mi, że x∊(2kπ;		+2kπ)
	2

Dobrze?

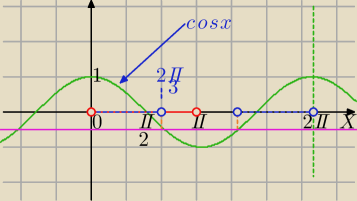
Mila: sinx>0 i cos(2x)−cosx<0 1) sinx>0 ⇔x∊(0+2kπ, π+2kπ) i 2) cos(2x)−cosx<0⇔ 2cos²x−1−cosx<0 , cosx=t i |t|≤1 2t²−t−1<0 Δ=9

	1−3		1+3
t=		lub t=
	4		4

	1
t=−		lub t=1
	2

	1
Parabola skierowana do góry⇔t∊(−		, 1)
	2

⇔

	1
−		<cosx<1
	2

Odczytuję część wspólną zbiorów (czerwony na osi i niebieski)

	2π
2kπ<x<		+2kπ
	3

Druga część w następnym wpisie, chyba, że masz rozwiązanie i nie trzeba.