planimetria, trudne zadania here vladimir: 1. Pole rombu jest równe 15, długość okręgu wpisanego w ten romb jest równa n√5. Oblicz obwód tego rombu. 2.W trapez równoramienny o kącie ostrym 30 stopni wpisano okrąg o promieniu 1,5. Oblicz długości podstaw tego trapezu. 3. Różnica między promieniem okręgu opisanego na kwadracie, a promieniem okręgu wpisanego w ten kwadrat jest równa 3. Oblicz pole tego kwadratu. Prosiłbym o jakąś pomoc, ponieważ nie wiem jak to zrobić. Prosiłbym także o rozpisanie krok po kroku tych zadań, z góry dzięki.

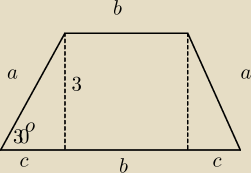
sowa.mądra.głowa: zad2. wysokośc ma 3, bo 1,5+1,5=3, teraz z własności na trójkąt 30stopni, 60stopni, 90stopni, mamy, że a=2*3=6, c= 3√3...teraz aby okrąg byl wpisany w czworokąt musi zajsc takie równanie: a+a=b+c+b+c, czyli 2a=2b+2c, czyli a=b+c, i podstawiamy 6=b+3√3, czyli pierwsza podstawa to b=6−3√3, druga podstawa to 2c+b, czyli 2*3√3+6−3√3=6+3p{3

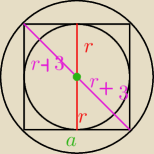
sowa.mądra.głowa: zad 3 bok a=2r, przekątna d=2r+6. wiemy ze przekatna kwadratu d=a√2, czyli d= (2r)√2, za d wstawiamy 2r+6, czyli 2r+6=(2r)√2, r+3=r√2, przenosząc r na jedną strone i obliczając, powinno Ci wyjsc r=3+3√2 czyli pole kwadratu to a²= (2r)²=(6+6√2)²

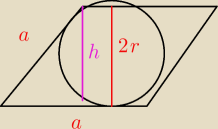
sowa.mądra.głowa: zad.1pole rombu=15, dł okregu=l=2πr 2πr=n√5 r=(n√5)/(2π) h=2r=2*[ (n√5)/(2π) ]=(n√5)/(π) pole rombu P=a*h P=a* (n√5)/(π) 15=a* (n√5)/(π) a=(15π)/(n√5) obw=4a=4*(15π)/(n√5) P.S. obrazek trochę nie wyszedł

vladimir: dzieki