Dowody
Jack:
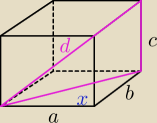
Mamy prostopadloscian, ktorego krawedzie maja dlugosci : a,b,c
d jest przekatna tego prostopadloscianu.
uzasadnij ze
a+b+c ≤ 3d
a więc...
z tw. Pitagorasa
x =
√a2 + b2
czyli
d
2 = c
2 + x
2 = c
2 + a
2 + b
2
(a+b)
2 + (a+c)
2 + (b+c)
2 = 2a
2 + 2b
2 + 2c
2 + 2ab + 2ac + 2bc
wiemy ze a
2 + b
2 ≥ 2ab, b
2+c
2 ≥ 2bc itd., więc
(a+b)
2 + (a+c)
2 + (b+c)
2 = 2a
2 + 2b
2 + 2c
2 + 2ab + 2ac + 2bc ≤
≤ 2a
2 + 2b
2 + 2c
2 + a2+b2 + a
2 + c
2 + b
2+c
2 =
= 4(a
2+b
2+c
2) = 4d
2
zatem
(a+b)
2 + (a+c)
2 + (b+c)
2 ≤ 4d
2
√(a+b)2 + (a+c)2 + (b+c) 2 ≤ 2d
tylko co teraz?
moze trzeba bylo ze wzoru
(a+b+c)
2 ? jednak wtedy mi sie nie zgadza...
22 mar 14:30
mar: A może coś z nierówności trójkąta skorzystać...
22 mar 15:25
Jack: Raczej nie pomoze...
22 mar 15:25
Kacper:

22 mar 16:02
jc: a2 + b2 + c2 = d2
s = a + b + c
0 ≤(s−3a)2 + (s−3b)2 + (s−3c)2 =
(s2 − 6sa + 9a2) + (s2 − 6sb + 9b2) + (s2 − 6sb + 9b2) =
3 s2 − 6s(a+b+c) + 9(a2+b2+c2) = 3s2 − 6s2 + 9 d2 = 9d2 − 3s2
stąd 3d2 ≥ s2, a+b+c = s ≤ d √3 < 3 d
Dowód, że a+b+c < 3d powinien być łatwiejszy.
22 mar 16:29
jc: I jest łatwiejszy...
d > a
d > b
c > c
3d > a+b+c
22 mar 16:33
jc: Uzupełnienie
d2 = a2 +b2 +c2 > a2 ⇒ d > a
d2 = a2 +b2 +c2 > b2 ⇒ d > b
d2 = a2 +b2 +c2 > c2 ⇒ d > c
dodajemy stronami i mamy 3d > a+b+c
22 mar 16:36
Jack: Skad wiedziales ze akurat
z −3a, potem − 3b itd... Post 16:29
22 mar 17:21
jc: Powtórzyłem dowód nierówności:
iloczyn skalarny wektorów u i v ≤ iloczyn długosci u i długości v
dla wektorów u=(a,b,c), v=(1,1,1).
A potem zobaczyłem, że dowodzimy słabszą nierówność.
Wystarczy dodadać stronami 3 nierówności: a < d, b < d, c < d.
Otrzymamy a+b+c < 3d.
Na koniec doadałem uzasadnienie nierówności: a < d, b < d, c< d.
22 mar 17:42
Jack: tak tak, ale chodzilo mi tylko oten
√3 a nie o samo 3

22 mar 18:08
 Mamy prostopadloscian, ktorego krawedzie maja dlugosci : a,b,c
d jest przekatna tego prostopadloscianu.
uzasadnij ze
a+b+c ≤ 3d
a więc...
z tw. Pitagorasa
x = √a2 + b2
czyli
d2 = c2 + x2 = c2 + a2 + b2
(a+b)2 + (a+c)2 + (b+c)2 = 2a2 + 2b2 + 2c2 + 2ab + 2ac + 2bc
wiemy ze a2 + b2 ≥ 2ab, b2+c2 ≥ 2bc itd., więc
(a+b)2 + (a+c)2 + (b+c)2 = 2a2 + 2b2 + 2c2 + 2ab + 2ac + 2bc ≤
≤ 2a2 + 2b2 + 2c2 + a2+b2 + a2 + c2 + b2+c2 =
= 4(a2+b2+c2) = 4d2
zatem
(a+b)2 + (a+c)2 + (b+c) 2 ≤ 4d2
√(a+b)2 + (a+c)2 + (b+c) 2 ≤ 2d
tylko co teraz?
moze trzeba bylo ze wzoru
(a+b+c)2 ? jednak wtedy mi sie nie zgadza...
Mamy prostopadloscian, ktorego krawedzie maja dlugosci : a,b,c
d jest przekatna tego prostopadloscianu.
uzasadnij ze
a+b+c ≤ 3d
a więc...
z tw. Pitagorasa
x = √a2 + b2
czyli
d2 = c2 + x2 = c2 + a2 + b2
(a+b)2 + (a+c)2 + (b+c)2 = 2a2 + 2b2 + 2c2 + 2ab + 2ac + 2bc
wiemy ze a2 + b2 ≥ 2ab, b2+c2 ≥ 2bc itd., więc
(a+b)2 + (a+c)2 + (b+c)2 = 2a2 + 2b2 + 2c2 + 2ab + 2ac + 2bc ≤
≤ 2a2 + 2b2 + 2c2 + a2+b2 + a2 + c2 + b2+c2 =
= 4(a2+b2+c2) = 4d2
zatem
(a+b)2 + (a+c)2 + (b+c) 2 ≤ 4d2
√(a+b)2 + (a+c)2 + (b+c) 2 ≤ 2d
tylko co teraz?
moze trzeba bylo ze wzoru
(a+b+c)2 ? jednak wtedy mi sie nie zgadza...

