 W trójkącie równoramiennym ramię ma długość 2, a kąt między ramionami ma miarę150o.
Podstawa tego trójkąta ma długość:
I powinno wyjść: 2√2 + √3
W odpowiedziach z twierdzenia cosinusów tak wyszło, ale sam robiłem wcześniej innym sposobem.
Powinno też dobrze wyjść, a jednak wyszło co innego:
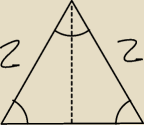
1) Narysowałem taki rysunek, i jeszcze na nim oznaczyłem:
− kąt 150o między ramionami mającymi długość 2.
− Na dole przy podstawie oba kąty oznaczyłem α = 15o .
− Całą podstawę oznaczyłem 2x.
− Przy przerywanej linii kąt 90o
2) Obliczenia:
cosα = x2 | *4
4cosα = 2x
2x = 4cosα
cosα = cos15 = cos(45 − 30) = cos45 * cos30 + sin45 * sin 30 =
= √22 * √32 + √22 * 12 =
= √2*√34 + √24 =
= √2*√3 + √24
2x = 4 * (√2*√3 + √24)
2x = √2 * √3 + √2
No więc mi wyszła podstawa √2 * √3 + √2 , a powinna wyjść: 2√2 + √3
Co zrobiłem źle ?
√6 + √2 tym bardziej źle
W trójkącie równoramiennym ramię ma długość 2, a kąt między ramionami ma miarę150o.
Podstawa tego trójkąta ma długość:
I powinno wyjść: 2√2 + √3
W odpowiedziach z twierdzenia cosinusów tak wyszło, ale sam robiłem wcześniej innym sposobem.
Powinno też dobrze wyjść, a jednak wyszło co innego:
1) Narysowałem taki rysunek, i jeszcze na nim oznaczyłem:
− kąt 150o między ramionami mającymi długość 2.
− Na dole przy podstawie oba kąty oznaczyłem α = 15o .
− Całą podstawę oznaczyłem 2x.
− Przy przerywanej linii kąt 90o
2) Obliczenia:
cosα = x2 | *4
4cosα = 2x
2x = 4cosα
cosα = cos15 = cos(45 − 30) = cos45 * cos30 + sin45 * sin 30 =
= √22 * √32 + √22 * 12 =
= √2*√34 + √24 =
= √2*√3 + √24
2x = 4 * (√2*√3 + √24)
2x = √2 * √3 + √2
No więc mi wyszła podstawa √2 * √3 + √2 , a powinna wyjść: 2√2 + √3
Co zrobiłem źle ?
√6 + √2 tym bardziej źle  @Edit: Po wymnożeniu na kalkulatorze wygląda na to, że wynik jest podobny, ale jak to
przekształcić ?
@Edit: Po wymnożeniu na kalkulatorze wygląda na to, że wynik jest podobny, ale jak to
przekształcić ?
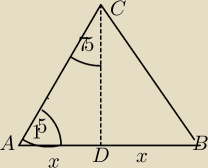 AB= 2*AD
AD=x
AC=2
AB= 2*AD
AD=x
AC=2
| x | |
= cos15 | |
| AC |
| √6+√2 | ||
cos15= | ||
| 4 |
| α | 1+cosα | |||
cos | = √ | |||
| 2 | 2 |
 Nie da się przekształcić ?
√6 + √2 do: 2√2 + √3
Nie da się przekształcić ?
√6 + √2 do: 2√2 + √3