rachunek różniczkowy Pixeleq: W prostopadłościanie długości krawędzi podstawy są w stosunku 1:2, a suma długości wszystkich krawędzi wynosi 60. Dobierz wymiary prostopadłościanu tak, abt jego objętość była jak największa. prosze o pomoc, z góry dzieki

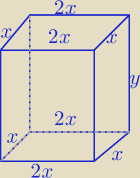
Mila: 4*x+4*2x+4y=60 /:4 x+2x+y=15 y=15−3x, 15−3x>0⇔x<5 i x>0 V=2x*x*y⇔ V(x)=2x²*(15−3x)=6*x²*(5−x) V(x)=6*(5x²−x³) V'(x)=6*(10x−3x²) V'(x)=0⇔10x−3x²=0 x*(10−3x)=0

	10
x=0∉D lub x=
	3

	10		10
x*(10−3x)>0⇔x∊(0,		)⇔ pochodna przy przejściu przez x =		zmienia znak z dodatniego
	3		3

na ujemny⇔

	10
Dla x=		funkcja V(x) osiąga maksimum lokalne.
	3

	10
Wymiary prostopadłościanu: y=15−3x=15−3*		=5
	3

10		20
	,		,5
3		3

	10		20		1000
Vmax=		*		*5=
	3		3		9