W trójkąt, którego boki mają długości
ola: W trójkąt, którego boki mają długości a, b, c wpisano okrąg i następnie
poprowadzono styczną do tego okręgu równoległą do boku o długości c, nie zawierającą
tego boku. Wykaż, że długość odcinka będącego częścią wspólną poprowadzonej stycznej i
trójkąta ma długość x= c(a+b+c)/ (a+b+c)
21 mar 19:10
===:
x= c(a+b+c)/ (a+b+c)

?
21 mar 19:19
ola: no tak

/ to kreska ułamkowa
21 mar 19:30
ola: albo przeprasazam, pomyliłam znak jeden
21 mar 19:31
ola: x= c*(a+b−c)/ (a+b+c)
21 mar 19:31
ola: ktoś ma jakiś pomysł?

21 mar 21:31
ola: pomożecie?

22 mar 09:27
===:
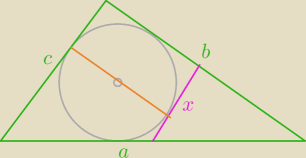
22 mar 11:05
yht:
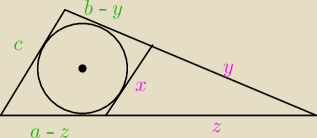
Duży trójkąt o bokach a,b,c jest podobny do trójkąta o bokach: z,y,x.
| | x | |
Skala podobieństwa to |
| |
| | c | |
stąd:
Z warunku wpisywalności okręgu w czworokąt:
c+x = a−z + b−y
c+x = a−a*{x}{c} + b−b*{x}{c}
i wychodzi co trzeba
22 mar 12:07
 ?
?
 / to kreska ułamkowa
/ to kreska ułamkowa



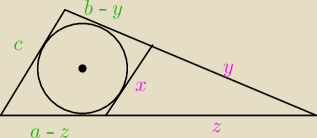 Duży trójkąt o bokach a,b,c jest podobny do trójkąta o bokach: z,y,x.
Duży trójkąt o bokach a,b,c jest podobny do trójkąta o bokach: z,y,x.