Kwadratowa poczatki 5-latek : Zadanie (tutaj mam problem ) Wyznacz funkcje kwadratowa jeżeli f(0)=f(2)=−3 i funkcja ta osiąga wartość najwieksza rowna 0 czy tu skorzystać z postaci ogolnej y=ax²+bx+c I tez podstawić wspolrzedne punktów (0,−3) i (2,−3) ? A potem ?

5-latek : No bo wtedy będziemy mieli −3= 0+0+c czyli −3=c mamy już lepsza postac y=ax²+bx−3 wstawiamy drugi punkt −3= 4a+2b

Metis:

	b
i f(		)=0
	2a

Janek191:

	0 +2
p =		= 1
	2

q = 0 więc f(x) = a*( x − 1)² + 0 f(0) = − 3 a*( 0 − 1)² + 0 = − 3 a = − 3 Odp. f(x) = − 3*( x − 1)²

5-latek : Chyba dzisiaj już nic nie wymysle Zebym miał a to x_w=p bym sobie policzyl z innego wzoru

5-latek : dzięki

5-latek : Metis jutro pomysle nad Twoim wpisem tez

Metis: Hmmm z niego chyba nic nie wyjdzie w tym przypadku.

	−b
Wiemy że p=
	2a

Zatem f(p)=q q w twoim przypadku to 0 − wartość największa Tam zjadłem minusa

Mila: Jeżeli f(0)=f(2) to oznacza że prosta :

	0+2
1) x=		=1 jest osią symetrii paraboli⇔
	2

2) x_w=1 3) f(1)=0⇔ p=1 i q=0 i a<0 I teraz postać kanoniczna

5-latek : Witam jeszcze raz Milu Patrzylem teraz na zbior zadań Gdowski Plucinski i tam sa tez ladne zadania z funkcji kwadratowej

5-latek : Milu A ten sposób co zaczalem robic to był dobry ? czy nie bardzo ?

Mila: Witaj, rozwiązuj z Anusiak, tam są łatwe i trudne.

5-latek : Tak wlasnie zauwazylem . On dużo eskpolatuje funkcje y=x²+px+q

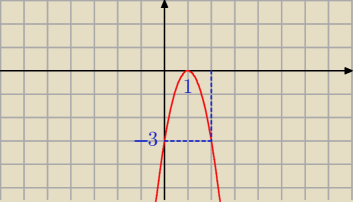
Mila: Dobrze, co widać na rysunku Janka, dalej musisz jednak obliczyć: x_w=1

−b
	=1⇔ f(1)=0
2a

b=−2a f(2)=4a+2b−3=−3 4a+2b=0 b=−2a f(x)=ax²−2ax−3 i f(1)=0 a−2a−3=0 a=−3 f(x)=−3x²+6x−3 ===========

kochanus_niepospolitus: 5−latek ... co do zadania Jeszcze przed rozpoczęciem rozwiązywania powinieneś parę rzeczy zauważyć: 1) Skoro NAJWIĘKSZA wartość jaką przyjmuje funkcja to 0, więc: 1.1) a < 0 1.2) funkcja posiada tylko jedno miejsce zerowe − można zapisać ją w postaci f(x)=a*(x−x₀)²

	|0 + 2|
2) f(0) = f(2) ... więc xwierzchołka =		= 1
	2

3) x_wierzchołka = x₀ Więc ... f(x) = a(x−1)² ... i pozostaje wyznaczenie a=−3

5-latek : Dobrze