Pochodne

Pochodne zef: Może ktoś mi podesłać pochodne do policzenia wraz z odpowiedziami ? Te z tej strony już przeliczałem a książki z pochodnymi nie mam :<

20 mar 20:13

Janek191: f(x) = e^2x*√x

20 mar 20:34

Janek191: f(x) = cos² (3 x)* sin x

20 mar 20:35

zef: Oj z tym "e" jeszcze nie liczyłem ale spróbuję

(e^2x)'*√x+e^2x*(√x)'

	1
e^2x(2x)'√x+e^2x*
	2√x

	e^2x
2e^2x*√x+
	2√x

	e^2x
2√xe^2x+
	2√x

I jak tam ?

20 mar 20:40

zef: 2cos(3x)*(−sin(3x))*sinx Nie liczyłem na aż takie trudne

20 mar 20:42

dero2005:

	2−√x
f(x) = log_√3
	2+√x

20 mar 20:52

ZKS: I oczywiście standard f(x) = x^x.

20 mar 20:56

zef: A coś z tych poprzednich mam dobrze ?

20 mar 20:57

ZKS: Pochodna z funkcji f(x) = e^2x • √x jest emotka

, natomiast kolejna już źle.

20 mar 21:02

zef:

	2−√x
log_√3*
	2+√x

1

2−√x

* (

)'

2−√x 
*In√3
2+√x 

2+√x

1

 * ((2−√x)'(2+√x)−(2−√x)(2+√x)'

2−√x 
*In√3
2+√x 

1

 * (−0,5x−1,5)(2+x0,5)−(2−√x)(0,5x−0,5)

2−√x 
*In√3
2+√x 

1

 * (−x−1,5−0,5x−1)−(x−0,5−1)

2−√x 
*In√3
2+√x 

(−x−1,5−0,5x−1)−(x−0,5−1)

2−√x 
*In√3
2+√x 

−x−1,5−0,5x−1−x−0,5+1

2−√x 
*In√3
2+√x 

Skończone

I tak jestem w szoku że ta pierwsza mi wyszła, bo dajecie masakrycznie trudne

20 mar 21:06

ZKS: Tej Ci nie sprawdzę, bo prosto w świecie mi się nie chce. emotka

20 mar 21:08

zef: a ja się tyle naliczyłem

20 mar 21:09

zef: Jakieś łatwiejsze pochodne bym poprosił bo zgodnie z podstawą to będę zaczynał je za rok a teraz robię małą rozgrzeweczkę

20 mar 21:10

dero2005: odpowiedź do 21;06

	−2
=
	(4−x)√xln√3

20 mar 21:11

zef: To śmiało można powiedzieć że byłem blisko emotka

, póki co to dla mnie jeszcze za wysoki poziom

20 mar 21:12

dero2005: f(x) = 8x^−7x = .......= −56x^−7x(lnx+1)

20 mar 21:14

zef: 8x^−7x=8(x^−7x) i po przykładzie :< To też jeszcze dla mnie za trudne.

20 mar 21:17

dero2005:

	21
f(x) = 3⁵√x⁷ = ......=		⁵√x²
	5

f(x) = e^sin²x = ...... = sin2xe^sin²x

20 mar 21:21

zef: 3(⁵√x⁷)' 3(x^7/5)' 7/5 * 3(x^2/5) 21/5(x^2/5) e^sin²x e^sin²x*(sin²x)' e^sin²x*2sinx*(cosx) e^sin²x*2sinxcosx

20 mar 21:25

5-latek : zef wypozycz sobie ksiazke albo kup Krysicki Wlodarski Analiza matematyczna w zadaniach cz 1

20 mar 22:39

zef: Szukałem ostatnio w bibliotece jakiejkolwiek książki do matematyki rozszerzonej ale póki co pustki. Odświeżam może ktoś coś rzuci jakimś przykładem

21 mar 19:09

PW: zef, jesteś typowym przykładem człowieka, który swoje kłopoty zwala na barki innych. Chcesz coś zrobić dla siebie, to rób.

21 mar 19:32

zef: (1+tg²x+tg³x)³ pochodna: 2(1+tg²x+tg³x)*(2tgx+3tg²x)*(1+tg²x+1+tg²x) Czy to jest dobrze zrobione ?

21 mar 20:07

PW: Nie. Powinno być 3(1 + tg²x+tg³x)²(2tgx(tgx)' + 3tg²x(tgx)') itd.

21 mar 20:14

zef: Mam pewną funkcję i mam wyznaczyć przedziały jej monotoniczności, więc liczę pochodną. Zostaje mi równanie stopnia drugiego wyznaczam x1 i x2 rysuję parabolę i wiem że malejąca jest poniżej osi x a rosnąca powyżej. Mam jedno pytanie kiedy jest przedział domknięty ?

21 mar 20:30

PW: ... rysuję parabolę i wiem że malejąca jest poniżej osi x a rosnąca powyżej. Fatalnym językiem opowiadasz − nie wiadomo o co idzie. Tu musi być precyzja wypowiedzi, wyraźnie trzeba powiedzieć o tym, jak monotoniczność funkcji zależy od znaku jej pochodnej. Na pytanie "kiedy jest przedział domknięty" nie umiem odpowiedzieć. Odpowiednie twierdzenie mówi o monotoniczności funkcji różniczkowalnej na przedziale otwartym.

21 mar 20:46

dero2005: Oblicz pochodną funkcji (dla wprawy)

	5−x²		1		5+x²		−20x
f(x) = √		= .........=		√		*
	5+x²		2		5−x²		25+10x²+x⁴

22 mar 10:17

dero2005:

	e^x+x³		3x²−x³
f(x) =		= ....... =
	4e^x		4e^x

22 mar 10:20

dero2005:

	1		√x		1
f(x) = sin²√		= ......... = −		*sin²√
	x		2x²		x

22 mar 10:24

zef:

	5−x²
1. [√		]'
	5+x²

1

−2x*(5+x2)−(5−x2)*2x

* (

)

 5−x2 
2√
 5+x2 

(5+x2)2

1

−20x

*

 5−x2 
2√
 5+x2 

(5+x2)2

1

−20x

*

 5−x2 
2√
 5+x2 

25+10x2+x4

22 mar 19:25

zef:

	e^x+x³
2. [		]'
	4e^x

(e^x+3x²)(4e^x)−(e^x+x³)(e^x)4

4e^x*4e^x

Tutaj mi się jedno 4e^x z mianownika skróci:

(e^x+3x²)−(e^x+x³)

4e^x

3x²−x³

4e^x

22 mar 19:32

zef:

	1
[sin²√		]'
	x

	1		1		1
2sin√		* cos √		* [√		]'
	x		x		x

	1		1		1
2sin√		* cos √		* (−		x^−1,5)
	x		x		2

Nie wiem czy tutaj jest dobrze :<

22 mar 19:36

zef: Może ktoś zerknąć ?

22 mar 19:45

Benny: to z sinusem git emotka

22 mar 19:47

zef: A mógłbyś napisać jak dalej z tego wybrnąć ? emotka

22 mar 19:49

Benny: Wybrnąć z czego?

22 mar 19:57

zef: Jak dojść do tej postaci:

	√x		1
−		*sin²√
	2x²		x

22 mar 19:59

Benny:

	1		−1		1		−√x
(−		x^−1,5)=		*		=
	2		2		√x³		2x²

	1		1		1
2*sin√		*cos√		=sin2√
	x		x		x

Tam raczej nie powinno być kwadratu emotka

22 mar 20:05

zef: Faktycznie, nie powinno być kwadratu emotka

Dzięki

22 mar 20:07

zef: Mam ciekawy przykład i nie wiem czy poradziłem sobie z nim

	6x
[e^cos²x * sin⁴√		]'=
	2+3x²

	6x
e^cos²x2cosx(−sinx) sin⁴√		+ e^cos²x *
	2+3x²

	6x		6x		6x
4sin³√		*cos√		*[√		]'=
	2+3x²		2+3x²		2+3x²

	6x
−e^cos²xsin2xsin⁴√		+ e^cos²x
	2+3x²

6x

6x

1

 *4sin3√

*cos√

*

*

2+3x2

2+3x2

 6x 
2√
 2+3x2 

	6(2+3x²)−6x(6x)

	(2+3x²)²

	6x
−e^cos²xsin2xsin⁴√		+ e^cos²x
	2+3x²

6x

6x

1

 *4sin3√

*cos√

*

*

2+3x2

2+3x2

 6x 
2√
 2+3x2 

	−18x²+12

	4+6x²+9x⁴

Zerknie ktoś ? emotka

22 mar 20:27

dero2005: Do ćwiczenia − pochodne

	1
f(x) = log₂(log₃x) = ............ =
	log₃x ln2*xln3

	1
f(x) = ln[ln(lnx)] = ............ =
	x ln(lnx) lnx

f(x) = x^¹_lnx = ........ = 0

22 mar 20:34

zef: log₂(log₃x)=?

	1		1		1
log₂(log₃x)=		*		=		Tak niepewnie ale wyszło
	xIn3		log₃xIn2		log₃xIn2*xIn3

	1		1		1		1
In[In(Inx)]=		*		*		=
	x		Inx		In(Inx)		xInxIn(Inx)

	1		1
x^¹_Inx=		x^¹_Inx(		)'
	Inx		Inx

	1		0*Inx−1/x(1)
x^¹_Inx=		x^¹_Inx (		)
	Inx		Inx²

	1		−1/x
x^¹_Inx=		x^¹_Inx
	Inx		Inx²

Nie wiem co dalej tutaj

22 mar 20:44

Benny: x^1/lnx=e^{lnx^1/lnx}=e lub

1
	=log_xe
lnx

x^log_xe=e

22 mar 20:53

zef: czyli wynik to e a nie 0 ?

22 mar 21:02

Benny: nieee wynik to 0 pochodna funkcji stałej to 0 przecież emotka

22 mar 21:04

zef: Czyli to co napisałeś to jest tylko uproszczenie i na koniec trzeba pochodną z e ? emotka

22 mar 21:06

dero2005:

	1
f(x) = 5^ln2x = ......... = 5^ln2xln5
	x

22 mar 21:07

Benny: Dokładnie tak zef

22 mar 21:09

zef: 5^In2x Hmm nie wiem z jakiego wzoru tutaj skorzystać

22 mar 21:10

zef:

	1
5^In2x=5^In2xIn5
	x

Dobra to było jednak proste

22 mar 21:12

dero2005:

	1		ak
f(x) =		= ............ = −
	ⁿ√(ax+b)^k		nⁿ√(ax+b)^k+n

22 mar 21:12

dero2005:

	x²+3x−2		−2x²−6x−13
f(x) =		= ............ =
	x²+x−5		(x²+x−5)²

22 mar 21:15

zef:

1
	=
(ax+b)^k/n

(ax+b)^−k/n −k/n*(ax+b)^−k/n*(ax+b)' −k/n*(ax+b)^−k/n*a

−k		1
	*		*a
n		(ax+b)^k/n−1

−ka

n(ax+b)^{k/n −1}

Hmm

22 mar 21:18

dero2005:

	7		8
f(x) = 8ln		= ........... = −
	2x+4		x+2

22 mar 21:19

zef:

x²+3x−2
	=
x²+x−5

(2x+3)(x²+x−5)−(x²+3x−2)(2x+1)

(x²+x−5)²

2x³+2x²−10x+3x²+3x−15−(2x³+x²+6x²+3x−4x−2)

(x²+x−5)²

2x³+2x²−10x+3x²+3x−15−2x³−x²−6x²−3x+4x+2

(x²+x−5)²

−2x²−6x−13

(x²+x−5)²

22 mar 21:22

zef:

	7
8In*		=
	2x+4

	2x+4
8*		Tutaj nie wiem
	7

22 mar 21:28

zef: Ref, pomoże ktoś z tą pochodną:

	7
8In*
	2x+4

22 mar 21:52

ICSP:

	2x + 4		−14		−8
= 8 *		*		=
	7		(2x + 4)²		x + 2

22 mar 21:54

Benny:

7
	=y
2x+4

	8
(8lny)'=		*y'
	y

22 mar 21:55

zef:

	7
Aj faktycznie trzeba jeszcze przemnożyć przez [		]' bo funkcja złożona, dziękuję
	2x+4

22 mar 21:56

zef: Odświeżam, jak ktoś coś ma może pisać emotka

22 mar 22:12

ICSP: ale czego potrzebujesz ?

22 mar 22:55

dero2005: Dla ćwiczenia f(x) = 2^5x*3^6x*x⁹ = ...............= 2^5x*3^6x(5ln2*x⁹+6ln3*x⁹+9x⁸)

23 mar 09:29

dero2005:

	5		5
f(x) = (		)^x = ...................= (		)^x(ln⁵_x−1)
	x		x

23 mar 09:34

zef: f=2^5x g=3^6x h=x⁹ f'g+fg'=z i później z'h+zh' Dobrze myślę ?

23 mar 15:37

Jerzy: Dobrze

23 mar 15:42

zef: Mam już pewne obliczenie ale nie wiem ile wynosi pochodna z 5In2, nie jestem pewien czy 0 ?

23 mar 15:51

Jerzy: 0

23 mar 15:53

zef: 2^5xIn2*5*3^6x+2^5x*3^6xIn3*6 2^5x5In2*3^6x+2^5x*3^6x*6In3=z z'h+zh' z=2^5x5In2*3^6x+2^5x*3^6x*6In3 z=[2^5x*5In2*3^6x]_z1+[2^5x*3^6x*6In3]_z2 pochodna z z1: [2^5x*5In2*5In2+2^5x*0] [(2^5x*5In2*5In2)'*3^6x+(2^5x*5In2*5In2)*(3^6x)'] [(2^5x*5In2+2^5x*0*3^6x+(2^5x*5In2*5In2)*3^6x*In3) [0+(2^5x*5In2*5In2)*3^6x*In3] pochodna z1=(2^5x*5In2*5In2)*3^6x*In3 pochodna z z2: z₂'=[2^5x*3^6x*6In3] 2^5x*5In2*3^6x+2^5x*3^6x*6In3=C i dalej: C'6In3+C*6(In3)' więc: 2^5x*5In2*5In2+2^5x*0 (2^5x*5In2*5In2)'*3^6x+(2^5x*5In2*5In2)*(3^6x)' 2^5x*5In2*5In2+0 (2^5x*5In2*5In2)'*5In2+(2^5x*5In2*5In2)*(5In2)' i tak skończyłbym z2

i na koniec (z1)'+(z2)'=z' z'h+zh' Może ktoś sprawdzić czy dobrze robiłem ?

23 mar 16:12

zef: Postaram się przeliczyć to bez takiego bałaganu aby mógł ktoś to sprawdzić emotka

2^5x*3^6x*x⁹ 2^5x=f 3^6x=g x⁹=H f*g*h Liczę więc pochodną, najpierw zajmę się tylko f i g (f*g)'=f'g+fg' Zatem podstawiam: (2^5x*3^6x)'=(2^5x)'*3^6x+2^5x*(3^6x)' Zajmuję się teraz prawą stroną równania: (2^5x)'*3^6x+2^5x*(3^6x)'= (2^5x*In2*5)*3^6x+2^5x*(3^6x*In3*6)= (2^5x*5In2)*3^6x+2^5x*(3^6x*6In3) I nazwę to jako (f*g)'=C Przechodzimy dalej i wracamy do H. C'H+CH' Podstawiamy: emotka

[(2^5x*5In2)*3^6x+2^5x*(3^6x*6In3)]'*x⁹+[(2^5x*5In2)*3^6x+2^5
x*(3^6x*6In3)]*(x⁹)']]= emotka

Z racji tego że jest dużo składników i trochę liczenia ponazywam sobie pewne wyrażenie(od lewej strony): a=(2^5x*5In2) b=3^6x c=2^5x d=3^6x*6In3 To są składniki z pierwszego nawiasu kwadratowego równania głównego (oddzielone serduchami

) z których liczę pochodną Zaczynam: a'=2^5x*5In2*5In2+0 b'=3^6x*6In3 liczę więc (a*b)'=a'b+ab' i podstawiam: (2^5x*5In2*5In2)*3^6x+(2^5x*5In2)*3^6x*6In3 Mam już połowę pochodnej z pierwszego nawiasu równania głównego Liczę 2 część pierwszego nawiasu równania głównego c'=2^5x*5In2 d'=3^6x*6In3*6In3+0 i liczę teraz (c*d)'=c'd+cd' i podstawiam: (3^6x*6In3*6In3)*2^5x+(3^6x*6In3)*3^6x*6In3 Policzyłem całą pochodną z pierwszego nawiasu równania głównego. Mam już prawie wszystko więc wracam do równania głównego i podstawiam:

{[(2^5x*5In2*5In2*3^6x)+(2⁵x*5In2*3^6x*6In3)]+[(3^6x*6In3*6In3*2^ {5x})+3^6x*6In3*2^5x*5In2)]}

x⁹+[(2^5x*5In2*3^6x+2^5x*3^6x*6In3)]*9x⁸ Pomiędzy wykrzyknikami jest pochodna z pierwszego nawiasu równania głównego. Pozostała tylko wyłączanie czynników przed nawias itd. Starałem się zapisać jak najbardziej zrozumiale, może ktoś sprawdzić

23 mar 17:06

zef:

	5
(		)^x=
	x

	5		5		5
(		)^x*In		*(		)'
	x		x		x

	5		5
(		)^x*In		*(−5/x²)
	x		x

Tutaj mi wyszło trochę inaczej, mógłby ktoś sprawdzić ten i poprzedni przykład

23 mar 17:20

dero2005:

	sinx		cosx
f(x) = (sinx+cosx)(tgx+ctgx) = .........=		−
	cos²x		sin²x

23 mar 19:14

dero2005: f'(x) = [(⁵_x)]' = [e^{ln(⁵_x)^x}]' = [e^xln⁵_x]' = e^xln⁵_x(xln⁵_x)' = = e^{ln(⁵_x)^x}[(x)'ln⁵_x+x(ln(⁵_x)'] =

	1
=(⁵_x)^x[1*ln⁵_x+x(		)*(⁵_x)']=
	⁵_x

= (⁵_x)^x[ln⁵_x+x(^x₅)(⁻⁵_x²)] = = (⁵_x)^x(ln⁵_x−1)

23 mar 19:36

zef: [(sinx+cosx)(tgx+ctgx)]'= 1 nawias pochodna: (sinx+cosx)'=cosx−sinx 2 nawias pochodna:

	1		1
(tgx+ctgx)'=		−
	cos²x		sin²x

f'g+fg'

	1		1
(cosx−sinx)(tgx+ctgx)+(sinx+cosx)(		−		)
	cos²x		sin²x

	sinx		1		1		cosx
cosxtgx+cosxctgx−sinxtgx−sinxctgx+		−		+		−
	cos²x		sinx		cosx		sin²x

	sinx		cosx		sinx		cosx
cosx*		+cosx*		−sinx*		−sinx*		+
	cosx		sinx		cosx		sinx

sinx		1		1		cosx
	−		+		−		=
cos²x		sinx		cosx		sin²x

cos2x

sin2x

sinx

1

1

cosx

sinx+

−

−cosx+

−

+

−

sinx

cosx

cos2x

sinx

cosx

sin2x

sin²x		cos²x		sin²x		cos²x
	+		−		−		+
sinx		sinx		cosx		cosx

sinx		1		1		cosx
	−		+		−		=
cos²x		sinx		cosx		sin²x

1		sin²x		cos²x		sinx		1		1
	−		−		+		−		+
sinx		cosx		cosx		cos²x		sinx		cosx

	cosx
−		=
	sin²x

	sin²x		cos²x		sinx		1
−		−		+		+
	cosx		cosx		cos²x		cosx

	cosx
−		=
	sin²x

	sin²x		cos²x		sinx		1		cosx
−(		+		)+		+		−		=
	cosx		cosx		cos²x		cosx		sin²x

−1		sinx		1		cosx
	+		+		−		=
cosx		cos²x		cosx		sin²x

sinx		cosx
	−
cos²x		sin²x

No no fajny przykład, ale się udało

24 mar 08:51

zef: Czekam na kolejne przykłady emotka

24 mar 09:24

Jerzy: y = 4arctg³(1/x) + 4x⁷*ln²(cos²x)

24 mar 09:56

dero2005:

	1
f(x) = arc cos¹_x = .....=
	√x⁴−x²

24 mar 10:21

dero2005: f(x) = (1+¹_x)^x = .........= (1+¹_x)^x [ln(1+¹_x)−¹_x+1]

24 mar 10:24

zef: 4(arctg³(1/x))+4x⁷*In²(cos²x)

	1
12arctg²(1/x)*(1/x)'
	1+x²

	−1		1
12arctg²(1/x)*(		)*
	x²		1+x²

	−1
12arctg²(1/x)*
	x²+x⁴

4x⁷*In²(cos²x)= 28x⁶*In²(cos²x)+4x⁷*(In²(cos²x))' 28x⁶*In²(cos²x)+4x⁷*(In(cos²x)*(In(cos²x))'

	1
(In(cos²x)*(In(cos²x))'=[		2cosx(−sinx)][In(cos²x)]+[In(cos²x)
	cosx

	1
*		2cosx(−sinx)]=
	cosx

(−2sinx)(In(cos²x))+(In(cos²x))(−2sinx) = pochodna z (In²(cos²x)) Więc podstawiam dalej: 28x⁶*In²(cos²x)+4x⁷*(−2sinx)(In(cos²x))+(In(cos²x))(−2sinx) I do początkowego równania:

	−1
12arctg²(1/x)*		+28x⁶In²(cos²x)+4x⁷(−2sinx)(In(cos²x))+(In(cos²x))(−2sinx)
	x²+x⁴

Wyszło mi coś takiego

24 mar 10:28

zef:

	1
arc cos
	x

−1		−1
	*
√1−x²		x²

1

√x⁴(1−x²)

1

√x⁴−x⁶

No mi wyszło trochę inaczej

24 mar 10:31

Jerzy:

	1
W pierwszej części popraw:
	1 + (1/x)²

	1
[ln²(cos²x)]' = 2ln(cos²x)*		2cosx(−sinx)
	cos²x

24 mar 10:43

zef:

	1
(1+		)^x
	x

	1		1		1
(1+		)^x*In(1+		)*(1+		)'
	x		x		x

	1		1		−1
(1+		)^x*In(1+		)*(		)
	x		x		x²

Hmm

24 mar 10:51

Jerzy: Źle licz pochodną iloczynu: x*ln(1 + 1/x)

24 mar 11:23

zef: In(1+1/x)+x(In(1+1/x))'

	1		−1
In(1+1/x)+x(		)*
	1+1/x		x²

	x		−1
In(1+1/x)+		*
	1+1/x		x²

	−x
In(1+1/x)+
	x²+x

teraz dobrze ?

24 mar 11:29

Jerzy: Jeszcze skróć przez x

24 mar 11:41

zef:

	−1
In(1+1/x)+
	x+1

24 mar 11:43

dero2005:

	x⁵
f(x) = ¹₅x⁵ arc cosx − ¹₄(x⁴+x³) = ......= x⁴ arc cosx −		− x³
	5√1−x²

	3
−		x²
	4

24 mar 12:04

zef:

1		1
	x⁵arc cosx −		(x⁴+x³)
5		4

1
	(x⁵arc cosx)'=
5

1		−1
	(5x⁴arccosx+x⁵		)
5		√1−x²

	−x⁵
x⁴arccosx+
	5√1−x²

	x⁵
x⁴arccosx−
	5√1−x²

1
	(x⁴+x³)
4

1
	(4x³+3x²)
4

	3x²
x³+
	4

	x⁵		3x²
x⁴arccosx−		−(x³+		)
	5√1−x²		4

	x⁵		3x²
x⁴arccosx−		−x³−
	5√1−x²		4

24 mar 12:13

dero2005:

	2√x+3
f(x) = √cosx − √x + 3√x = ...= − sinx−
	4√x²+3x√x

24 mar 13:32

zef:

	1		−sinx
√cosx=		*(−sinx)=
	2√cosx		2√cosx

	1
√√x=x^1/4=1/4x^−3/4=
	√√(0,25x)³

	1
√3√x=3^1/2x^1/4=√3(x)^1/4=√31/4x^−3/4=		*√3
	√√(0,25x)³

−sinx		1		1
	−		+		*√3
2√cosx		√√(0,25x)³		√√(0,25x)³

−sinx		√3−1
	+
2√cosx		√√(0,25x)³

Wyszło mi coś takiego

Czy w taki sposób mogę liczyć ?

24 mar 14:10

dero2005: Dla tej funkcji z 13:32 zaszła pomyłka w odpowiedzi

	1		2√x+3
..=		*(−sinx−		)
	2√cosx−√x+3√x		4√x²+3x√x

Przyjmij y = x+3√x z = cosx − √x + 3√x

24 mar 14:45

zef: √cosx−√x+3√x

1		1		−3
	*[(−sinx)−		*(		)]
2√cosx−√x+3√x		2x		x²

1		3
	*[(−sinx)+		]
2√cosx−√x+3√x		2x³

Coś takiego mi tylko do głowy przychodzi ale jest chyba źle

24 mar 16:25

dero2005:

	3
y' = (x+3√x)' = x' + 3(√x)' = 1+
	2√x

	1
z' = (cosx − √x+3√x)' = (cosx − √y)' = (cosx)' − (√y)' = −sinx −		*y' =
	2√y

	1		3
−sinx −		*(1+		) =
	2√x+3√x		2√x

	1		2√x+3
= − sinx −		*
	2√x+3√x		2√x

	1
f'(x) = (√z)' =		*z' = dokończ
	2√z

24 mar 17:02

dero2005:

	1
f(x) = sinx −		cos⁴x = .....= cosx + 2sinx cos³x
	2

25 mar 12:04

zef: sinx − 1/2cos⁴x= cosx−2cos³x*(−sinx) cosx+2cos³xsinx

25 mar 13:08

zef:

1
	(arsinh(x)+x√x²+1)
2

1
	*In(x+√x²+1)+
2

	1		x²+1
pochodna z √x²+1=		*x²+1=
	2√x²+1		2√x²+1

pochodna z x=1 więc: x√x²+1=

	x²+1
√x²+1+x*		=
	2√x²+1

	x³+x
√x²+1+
	2√x²+1

końcowy wynik to:

1		x³+x
	*In(x+√x²+1)+ √x²+1+
2		2√x²+1

Dobrze ?

25 mar 13:18

zef: Ups tam jeszcze razy 1/2 musi być bo to zgubiłem

25 mar 13:20

zef: Czyli wynik to:

1		√x²+1		x³+x
	*In(x+√x²+1)+		+
2		2		4√x²+1

25 mar 13:21

zef: No to poprawiam po kolei:

	2x		x
[√x²+1]'=		=
	2√x²+1		√x²+1

czyli arsinh(x)=In(x+√x²+1) i z tego muszę liczyć pochodną ? Ja myślałem że podałeś mi już gotową pochodną

25 mar 13:25

zef: No masz rację

Już biorę się do roboty.

25 mar 13:27

zef:

1
	(arsinh(x)+x*√x²+1)
2

pochodna z arsinh(x)= [In(x+√x²+1)]'=

	x
In(1+		)
	√x²+1

pochodna z x*√x²+1

	x²
√x²+1+
	√x²+1

Więc wynik to:

1		x		x²
	(In(1+		)+√x²+1+		)
2		√x²+1		√x²+1

Hmm a teraz ?

25 mar 13:31

zef: arsinh(x)=In(x+√x²+1) Chyba zapomniałem o tym "In"

1		x
	*(1+		)
x+√x²+1		√x²+1

1		x+√x²+1
	*(		)
x+√x²+1		√x²+1

1

√x²+1

No w końcu wyszło

Reszta się zgadzała ?

25 mar 13:37

zef:

1		1		x²
	(		+√x²+1+		)
2		√x²+1		√x²+1

1		√x²+1		x²
	+		+
2√x²+1		2		2√x²+1

x²+1		√x²+1
	+
2√x²+1		2

Biorę się za następny przykład

25 mar 13:41

zef:

	1
[		(arcsin(x)+x√1−x²)]'
	2

	1
[arcsin(x)]'=
	√1−x²

[x√1−x²]'= [x]'=1

	1		−2x		−x
[√1−x²]'=		*(−2x)=		=
	2√1−x²		2√1−x²		√1−x²

zatem [x√1−x²]'=

	−x²
√1−x²+
	√1−x²

	1
[		(arcsin(x)+x√1−x²)]'=
	2

1		1		−x²
	(		+√1−x²+		)
2		√1−x²		√1−x²

1		1−x²
	(		+√1−x²)
2		√1−x²

1		1−x²		(√1−x²)
	(		+		)
2		√1−x²		√1−x²

1		1−x²		1−x²
	(		+		)
2		√1−x²		√1−x²

1		2−2x²
	(		)
2		√1−x²

2−2x²

2√1−x²

1−x²

√1−x²

gotowe

25 mar 13:51

dero2005:

	√x²+1−x		−2
f(x) = log_¹₂		= ....=
	√x²+1+x		√x²+1*ln¹₂

25 mar 13:52

zef:

	√x²+1−x
[log_¹₂		]'
	√x²+1+x

1

*pochodna tego ilorazu

 √x2+1−x 1 
[
]*In
 √x2+1+x 2 

	√x²+1−x
[		]'=
	√x²+1+x

licznik pochodna:

1
	*2x−1
2√x²+1

x
	−1
√x²+1

mianownik pochodna:

	x
√x²+1+x=		+1
	√x²+1

pochodna z ilorazu(dzielone przez kwadrat mianownika, to dopisałem na koncu):

	x		x
(		−1)*(√x²+1+x)−(√x²+1−x)(		+1)
	√x²+1		√x²+1

x(√x²+1+x)		x(√x²+1−x)
	−(√x²+1+x)−[		+(√x²+1−x)]
√x²+1		√x²+1

x(√x²+1+x)		x(√x²+1−x)
	−(√x²+1+x)−		−(√x²+1−x)
√x²+1		√x²+1

	x√x²+1+x²		x√x²+1−x²
−2(√x²+1+x)+		−
	√x²+1		√x²+1

	x√x²+1+x²−x√x²+1−x²
−2(√x²+1+x)+
	x√x²+1

−2(√x²+1+x)
	=
(√x²+1+x)²

−2

√x²+1+x

Końcowy wynik:

1

−2

*

 √x2+1−x 1 
[
]*In
 √x2+1+x 2 

√x2+1+x

−2

(√x²+1−x)In1/2

Ale mordęga

Wynik się minimalnie różni, czy na pewno odpowiedź jest dobra ?

25 mar 14:18

dero2005: Odpowiedź jest dobra

25 mar 14:34

zef: To gdzie jest u mnie błąd, niby minimalny ale jest :<

25 mar 14:34

zef: Jestem prawie pewien że jest dobrze.

25 mar 14:38

zef: ref

26 mar 10:21

dero2005:

	5tg⁴√x
f(x) = tg⁵√x = ..=
	2√x cos²√x

26 mar 10:39

Benny: @zef Na samym początku uprość sobie wyrażenie logarytmowane.

26 mar 10:42

dero2005: f(x) = x³ e^4x cosx = ...= 3x²e^4x cosx + 4x³e^4x cosx − x³e^4x sinx

26 mar 10:43

zef: tg⁵√x=

	1		1
5tg⁴√x*		*		=
	cos²(√x)		2√x

5tg⁴√x

2√x*cos²√x

26 mar 11:16

Jerzy: Dobrze

26 mar 11:18

zef: x³e^4xcosx [x³]'=3x² [e^4x]'=e^4x*4=4e^4x [cosx]'=−sinx [3x²*e^4x+x³*e^4x*4e^4x]' 6x*e^4x+3x²*4e^4x+[3x²*e^4x+x³*4e^4x]'*4e^4x 6x*e^4x+3x²*4e^4x+[6x*e^4x+3x²*4e^4x+3x²*4e^4x+16e^4x]4e^4x+ [3x²*e^4x+x³*4e^4x]16e^4x i teraz bym dał z tego pochodną *cosx+to* pochodna z cosx ale wyszlo mi tego za duzo

26 mar 11:34

Jerzy: Już na początku żle... [x³e^4x]' = 3x²e^4x + x³*4e^4x

26 mar 11:40

zef: Faktycznie, jak piszę na komputerze a nie na kartce to zawsze coś namieszam :< Ale czy nie ma krótszej drogi na obliczenie tego ? Można się zaliczyć na śmierć

26 mar 11:42

zef: Policzę to jeszcze raz ale najpierw na kartce, a później przepiszę emotka

26 mar 11:43

Jerzy: f'(x) = (3x²e^4x + x³*4e^4x)*cosx − x³e^4x*sinx

26 mar 12:27

dero2005:

	10
f(x) = −5cos⁴*¹₆x = ...... =		(cos¹₆x)³*sin¹₆x
	3

	2		−6cosx
f(x) =		= .... =
	sin³x		sin⁴x

26 mar 13:03

zef: Nie wiem czy dobrze liczę tą pochodną

x³e^4xcosx i ja bym to zrobił tak: k=[x³]'=3x² l=[e^4x]'=4e^4x m=[cosx]=−sinx k'l+kl'=C C'm+Cm' Więc podstawiam: C=3x²*e^4x+x³*4e^4x C'=6xe^4x+3x²*4e^4x+3x²4e^4x+x³16e^4x C'm+Cm'= [6xe^4x+3x²*4e^4x+3x²4e^4x+x³16e^4x]cosx+[3x²*e^4x+x³*4e^4x](−sinx) Dobrze myślę ?

26 mar 13:04

Jerzy: Napisałem Ci tą pochodną o 12:27

26 mar 13:05

zef: Hmm to co ja źle robię ?

26 mar 13:06

dero2005:

	arc sinx		arc cosx + arc sinx
f(x) =		= ...... =
	arc cosx		√1 − x² (arc cosx)²

26 mar 13:07

Jerzy: K(x) = x³*e^4x f(x) = K(x)*cosx f'(x) =[K(x)]'*cosx + K*(cosx)' ... .jedna linijka

26 mar 13:11

zef: −5cos⁴(1/6x)= −(5cos⁴(1/6x))= −(20cos³(1/6x)*(−sin(1/6x))*1/6) 20cos³(1/6x)*(sin(1/6x))*1/6

10
	cos³(1/6x)(sin(1/6x))
3

26 mar 13:11

zef: Czyli po prostu za dużo liczyłem

2
	=
sin³x

−2(sin³x)'

(sin³x)²

U{−2(3sin²x)(cosx){(sin⁶x}

−6sin²x(cosx)

sin⁶x

−6cosx

sin⁴x

26 mar 13:14

zef:

arcsinx
	=
arccosx

1 −1 
(arccosx)−(arcsinx)(
)
√1−x2 √1−x2 

arccosx2

arccosx arcsinx 
+
√1−x2 √1−x2 

arccosx2

arccosx+arcsinx

√1−x²(arccosx)²

26 mar 13:19

Jerzy: ostatnia łatwiej liczyć tak: f(x) = 2*sin⁻³x i f'(x) = 2*(−3)sin^−4x*cosx

26 mar 13:21

zef: No w sumie

Ale tam chyba sin⁻⁴ a nie −4x emotka

26 mar 13:22

Jerzy: tak ... −4

26 mar 13:23

Jerzy: zapis: arccosx² ... niewłaściwy

26 mar 13:37

zef: Oj no tam w moim zamyśle jest nawias i kwadrat poza nawiasem

26 mar 13:37

Jerzy: oceniajacy ocenia to co widzi

26 mar 13:39

dero2005:

	5		x³
f(x) = arc sin√x⁵ = ... =		√
	2		1−x⁵

	1
f(x) = log₇ tg(¹₃π + ¹₂x) = .... =
	sin(²₃π + x) ln7

26 mar 14:48

zef: arc sin^5/2

1
	*5/2x^3/2
√1−x⁵

5√x³
	=
2√1−x⁵

5		x³
	*√
2		1−x⁵

26 mar 15:02

zef: log₇tg(1/3π+1/2x)=

1		1
	*		*(1/3π+1/2x)'=
tg(1/3π+1/2x)In7		cos²(1/3π+1/2x)

1		1
	*		*(0+1/2)=
tg(1/3π+1/2x)In7		cos²(1/3π+1/2x)

1		1
	*		*1/2=
tg(1/3π+1/2x)In7		cos²(1/3π+1/2x)

1		1
	*		*1/2
sin/cos(1/3π+1/2x)In7		cos²(1/3π+1/2x)

1

2sincos(1/3π+1/2x)In7

1

sin[2(1/3π+1/2x)]In7

1

sin(2/3π+x)In7

26 mar 15:08

zef: Ref

26 mar 18:38

dero2005:

	x+3		3
f(x) = log₄√		= ...=
	3−x		(9−x²)*ln4

26 mar 19:48

dero2005:

	sinx + tg²x
f(x) = 8ln tg ²₃x +		= ...
	2x − 3

	32		(cos³x+2 tg x)(2x − 3)− 2sinx cos²x−2 sin²x
=		+
	3sin⁴₃x		(2 x − 3)² *cos²x

26 mar 19:58

zef:

	x+3
[log₄√		]'
	3−x

1

1

x+3

*

]*[

]'

 x+3 
√
In4
 3−x 

 x+3 
2√
 3−x 

3−x

1

1

1(3−x)−(x+3)(−1)

*

]*[

]

 x+3 
√
In4
 3−x 

 x+3 
2√
 3−x 

(3−x)2

1

1

3−x+x+3

*

]*[

]

 x+3 
√
In4
 3−x 

 x+3 
2√
 3−x 

(3−x)2

1

1

6

*

]*[

]

 x+3 
√
In4
 3−x 

 x+3 
2√
 3−x 

(3−x)2

1

1

3

*

]*[

]

 x+3 
√
In4
 3−x 

 x+3 
√
 3−x 

(3−x)2

1

3

*[

]

x+3 
In4
3−x 

(3−x)2

3

(9−x²)*In4

26 mar 20:02

zef:

	2		sinx+tg²x
8In tg(		x) +
	3		2x−3

	2
8In tg(		x)=z
	3

sinx+tg²x
	=y
2x−3

	2
z'=[8In tg(		x)]'
	3

	2
[8(In tg(		x))]'
	3

1

1

2

8(

*

*

)

 2 
tg(
x)
 3 

cos2x

3

2

8(

)

 sin 2 
(
)(
x)*cos2x*3
 cos 3 

2

8(

)

 2 
3(sincos)(
x)
 3 

16

3sincos(2/3x)

32

6sincos(2/3x)

32

3sin(4/3x)

	sinx+tg²x
y'=[		]'
	2x−3

[sinx+tg²x]'(2x−3)−(sinx+tg²x)[2x−3]'

(2x−3)²

 1 
[cosx+2tgx*
](2x−3)−(sinx+tg2x)*2
 cos2x 

(2x−3)2

 1 
[cosx+2([sinx/cosx]*
)(2x−3)−(sinx+tg2x)*2
 cos2x 

(2x−3)2

 1 sin2x 
[cosx+2([sinx/cosx]*
)(2x−3)−(sinx+
)*2
 cos2x cos2x 

* cos2x/cos2x

(2x−3)2

(cos³x+2tgx)(2x−3)−(sinxcos²x+sin²x)2

(2x−3)²cos²x

(cos³x+2tgx)(2x−3)−(2sinxcos²x+2sin²x)

(2x−3)²cos²x

(cos³x+2tgx)(2x−3)−2sinxcos²x−2sin²x

(2x−3)²cos²x

Więc odpowiedź to z'+y':

32		(cos³x+2tgx)(2x−3)−2sinxcos²x−2sin²x
	+
3sin(4/3x)		(2x−3)²cos²x

26 mar 20:22

Jack:

	x²−x		1
f(x) =		+ cos2α −		sinα
	3x+1		2

zrob z tego pochodna : D ps. zdajesz mature w tym roku a juz liczysz pochodne z e oraz ln ?najs...

26 mar 20:36

ZKS:

	(3x + 1)(2x − 1) − 3(x² − x)
f'(x) =
	(3x + 1)²

	(3x − 1)(x + 1)
f'(x) =
	(3x + 1)²

26 mar 20:52

zef: Maturę zdaję za rok, teraz jestem w 2 klasie liceum emotka

α=z (dla ułatwienia)

	x²−x		1
[		+cos2z−		sinz]'
	3x+1		2

x²−x
	=k
3x+1

cos2z=l

1
	sinz=m
2

Zaczynamy od k

	x²−x
k'=[		]'
	3x+1

(2x−1)(3x+1)−(x²−x)(3)

(3x+1)²

(6x²+2x−3x−1)−(3x²−3x)

(3x+1)²

6x²−x−1−3x²+3x

(3x+1)²

3x²+2x−1
	=k'
(3x+1)²

hmm pochodna l' i m' będą wynosiły 0 bo tu nie widzę zmiennej x. Zatem odpowiedź to:

3x²+2x−1

(3x+1)²

26 mar 20:54

zef: @Jack Do końca 2 klasy liceum zamierzam ogarnąć pochodne i całki, a chyba to nie jest niemożliwe

26 mar 21:01

zef: [5x²*e^−3x]' 10x*e^−3x+5x²*(e^−3x*−3) 10x*e^−3x+5x²*(−3e^−3x) e^−3x(−15x²+10x)

27 mar 12:36

zef: Wracam do pochodnej z którą wcześniej sobie nie poradziłem

[cos²(3x)*sinx]' [cos²(3x)]'sinx+cos²(3x)[sinx]' [2cos(3x)*(−sin3x)*3](sinx)+cos²(3x)(cosx) [2cos(3x)*(−3sin3x)](sinx)+cos²(3x)(cosx) [−6cos(3x)*sin(3x)](sinx)+cos²(3x)(cosx) [−(6cos(3x)*sin(3x)](sinx)+cos²(3x)(cosx) [−3sin(6x)](sinx)+cos²(3x)(cosx) Dobrze ? emotka

27 mar 12:43

Jack: niestety nie...

27 mar 12:48

zef: Coś pewnie zgubiłem ? emotka

27 mar 12:49

Benny: Ok emotka

27 mar 12:49

Jack: przejscie z przedostatniej do ostatniej jest nie tak

27 mar 12:50

Benny: Czemu niby?

27 mar 12:51

zef: Co tu jest nie tak ?

27 mar 12:51

Jack: dobra nie wazne, niby jest git... emotka

27 mar 12:53

zef: @Benny Masz jeszcze może jakąś fajną pochodną do policzenia ? I czy trudno jest nauczyć się całek jeśli będę umiał dobrze pochodne ?

27 mar 12:54

Jack: a po co Ci calki...zespolonych sie naucz

27 mar 12:55

zef: Też mam w planach ale póki co nie umiem jeszcze podstaw z trygonometrii (nie miałem tego jeszcze). Chodzi mi o te zadania typu rozwiąż równanie w przedziale i wynik jest z tymi wielokrotnościami "k", tego będę się musiał najpierw nauczyć.

27 mar 12:57

Jack:

	1
sinx =
	2

x = ... oto chodzi?

jak chcesz koniecznie pochodne to mozesz jeszcze wielu zmiennych pochodna po x, po y itd... ale najpierw sie naucz tego co wymagaja na maturze emotka

27 mar 12:59

zef: No i z tego co napisałeś to wiem jedynie że x=30^o Ale przecież są jeszcze inne ćwiartki więc wynik pewnie nie będzie tylko 30^o A co jest z pochodnych wymagane na maturze ? Coś trudniejszego ?

27 mar 13:02

Kasia niezdara: boze toc to kody CIA

27 mar 13:06

Kasia niezdara: boze toc to kody CIA

27 mar 13:06

zef: Eeee bez przesady

27 mar 13:07

Benny: Zespolone szybko idzie się nauczyć, jeśli masz opanowane wielomiany. Jeśli dobrze ogarniasz pochodne to całki nieoznaczone nie powinny sprawiać problemu, bo od razu będzie zauważał podstawienia lub pochodne w funkcjach podcałkowych. Masz jedną, nic fajnego nie mogę znaleźć. f(x)=−ln(1−x+√5−2x+x²)

27 mar 13:08

ZKS: Schemat rozwiązywania dla równań typu sin(x) = sin(y) jest następujący x = y + k • 2π ∨ x = π − y + k • 2π.

27 mar 13:08

zef: [−In(1−x+√5−2x+x²)]' {−[In(1−x+√5−2x+x²)]}'

	1
−		*[1−x+√5−2x+x²]'
	1−x+√5−2x+x²

	1		1
−		*[0−1+		*(5−2x+x²)']
	1−x+√5−2x+x²		2√5−2x+x²

	1		1
−		*[−1+		*(−2+2x)]
	1−x+√5−2x+x²		2√5−2x+x²

	1		−2+2x
−		*[−1+		]
	1−x+√5−2x+x²		2√5−2x+x²

	1		−2+2x−2√5−2x+x²
−		*[		]
	1−x+√5−2x+x²		2√5−2x+x²

2−2x+2√5−2x+x²

(2√5−2x+x²)(1−x+√5−2x+x²)

Pewnie wynik powinien być w jakiejś ładniejszej postaci ? emotka

27 mar 13:20

Jack: z pochodnych na maturze same banaly...aczkolwiek nie ma do liczenia pochodnej tylko od tego sa zadania optymalizacyjne... Wyznacz maxymalne/minimalne pole, objetosc, dlugosci krawedzi rombu, graniastoslupa itd. pochodne sa zawsze od max/min... Maksymalna wartosc w przedziale, minimalna cena w sklepie itd. W tych zadaniach co tam wrzucilem (8 zadan) to tam wlasnie sie je wykorzystuje liczysz pochodna, przyrownujesz do zera i masz ekstrema

27 mar 13:20

ZKS: Niestety, samo zerowanie się pochodnej nie oznacza, że w tym punkcie jest ekstremum.

27 mar 13:22

Jack: naturalnie sa 2 warunki, drugim jest zmiana znaku, ale nie przyszedlem tu opisywac jak to wszystko dziala emotka

27 mar 13:26

zef: @ZKS Z samego schematu nic nie wywnioskuje :<

27 mar 13:26

ZKS: Dużo można wywnioskować, jeżeli wie się chociaż jak wygląda wykres sinusa.

27 mar 13:27

zef: No wartości powtarzają się co 2π

27 mar 13:28

Jack:

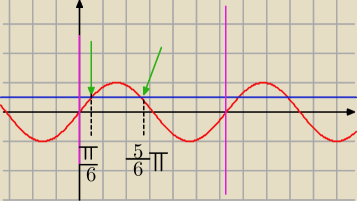
	1
Niebieska −>> y =
	2

Różowa −> Okres sinusoidy Czerwona −> wykres funkcji sinus

	1
jak widac sin przyjmuje		w dwoch miejsach w jednym okresie (zielone strzalki)
	2

	1
sin 30 =
	2

ale takze

	1
sin (180−30) =
	2

pozniej bedziesz ze wzorow redukcyjnych wszystko jechal..., ale na razie po prostu odczytujesz z wykresu na wykresie oznacza sie jako π, gdzie π wynosi 180 stopni(radiany i te sprawy emotka

27 mar 13:35

zef: No to wszystko rozumiem. Czyli π−x1=x2 ?

27 mar 13:38

Benny: Wynik do tamtej pochodnej to:

1

√x²−2x+5

27 mar 14:56

Benny: Skróć przez dwa i licznik z mianownikiem emotka

27 mar 15:03

zef: ref

28 mar 13:41

dero2005:

	2		5
f(x) = 5ln		= .. =
	x−√x²−1		√x²−1

28 mar 14:20

zef:

	2
5(In		)'
	x−√x²−1

	x−√x²−1		2
5(		)*(		)'
	2		x−√x²−1

	x−√x²−1		−2(x−√x²−1)'
5(		)*(		)
	2		(x−√x²−1)²

x−√x2−1

 x 
−2(1−
)
 √x2−1 

5(

)*(

2

(x−√x2−1)2

x 
−1
√x2−1 

5(x−√x2−1)*

(x−√x2−1)2

x 
−1
√x2−1 

5*

(x−√x2−1)

	x−√x²−1		1
5*(		)*
	√x²−1		x−√x²−1

5

√x²−1

29 mar 18:30