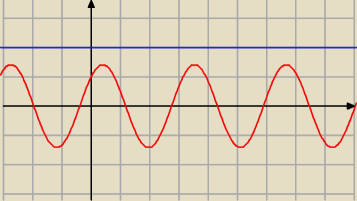
równanie klaraxx: rozwiąż równanie: cos 2x + sin 2x= 2 Godzinę się mecze, stosuje wzory na podwojony kąt i nie wychodzi mi proszę o pomoc..

klaraxx: Ktoś coś?

Janek191: cos 2 x = sin 2 x = 2 = 2*(sin² x+ cos² x) =2 sin² x +2 cos² x

5-latek : No to już ma Pani profesor odpowiedz . Ktoś coś

tss: max(sin(α)+cos(α))=√2

klaraxx: Janek, tak właśnie robię, ale utykam cały czas, nie mogę niczego wyciągnąć przed nawias ani doliczyć rozwiązałbyś do końca?

tss: rozwiązanie to x∊{Φ}

ICSP: cos(2x) = 1 + (sinx −cosx)² Równość może zajśc tylko gdy cos2x = 1 i sinx − cosx = 0 Równanie jest sprzeczne.

Janek191:

tss: sin(2x)+cos(2x)=2 //()² sin²(2x)+2sin(2x)cos(2x)+cos²(2x)=4 2sin(2x)cos(2x)=3 sin(4x)=3>1 ⇒x∊{Φ}

klaraxx: mhm...ech a ja liczyłam...próbowałam grupować...Wy widzicie od razu że to sprzeczność?

klaraxx: tss, możemy podnieść do kwadratu nie znając znaku lewej strony?

tss: Oczywiście, że nie. Tylko dla założenia L>0

ida: Ok, a czy do tej sprzeczności daloby sie dojsc o prostu licząc i próbując rozwiązać ten przykład z wzorów trygonometeycznych?

ida: (Tu klaraxxx z telefonu )

ida: Ale dobra,juz wszystko wiem dziękuję za pomoc