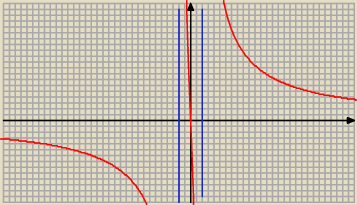
Pochodne funkcji (monotoniczność) Uneur: Wyznacz maksymalne przedziały monotoniczności funkcji f, jeśli f(x)=100x/(x²−4) Obliczyłem: Df=R−{−2,2} f'(x)=[(100x)'*(x²−4)−(x²−4)'*100x]/[(x²−4)²]=[100x²−400−200x²]/[(x²− 4)²]=[−100x²−400]/[(x²−4)²] Nie wiem jak wyznaczyć miejsca zerowe, bo nauczyciel mówił żeby lepiej nie rozbijać mianownika przy obliczaniu funkcji z ułamków (więc nie wyjdzie funkcja kwadratowa), a co za tym idzie nie potrafię zrobić rysunku pomocniczego, by określić monotoniczność i określić dziedziny Df'. Pomoże ktoś w dalszych obliczeniach?

Jerzy: interesuje Cię jedynie znak trójmianu: −100x² − 400 , bo mianownik jest zawsze dodatni

Uneur: Ale dajmy na to że x=2, wtedy całość się zeruje (to samo dla x=−2), więc musi istnieć dziedzina.Tylko czy z czegoś jeszcze się składa?

Janek191:

	100 x
f(x) =
	x2 − 4

więc

	100(x2 − 4) − 100x*( 2 x)		100x2 − 400 − 200 x2
f '(x) =		=		=
	(x2 − 4)2		(x2 −4)2

	− 100 x2 − 400
=		< 0 dla x ∊ ℛ \{ − 2, 2}
	(x2 −4)2

Funkcja f maleje w : ( − ∞, − 2) , ( − 2, 2), ( 2 , +∞)