granice funkcji gf:

	3x2−5x−2
lim x−>2
	5x2−20

Jak to rozwiązać? Po podstawieniu wychodzi symbol nieoznaczony. Wyciąganie przed nawias nic mi nie dało, bo wyszedł zły wynik.

Jerzy: a próbowałeś rozłożyć licznik na czynniki ?

gf: Teraz zauważyłem, że w mianowniku moge wyciągnąć 5 co da mi możliwość skorzystania ze wzoru a²−b². Co do licznika, to nie bardzo wiem jak to rozłożyć. Delte mam pliczyć?

Janek191:

	1
3 x2 − 5 x − 2 = 3*( x +		)*( x − 2) = ( 3 x + 1)*(x − 2)
	3

bo Δ = 25 − 4*3*(−2) = 25 + 24 = 49 √Δ = 7

	5 − 7		1		5 + 7
x1 =		= −		x2 =		= 2
	6		3		6

5 x² − 20 = 5*( x² − 4) = 5*( x −2)*(x + 2) zatem

	3 x + 1
f(x) =
	5*(x + 2)

zatem

	3*2 + 1		7
lim f(x) =		=
	5*(2 + 2)		20

x→2

gf: A ten? podobny przykład:

	2x3+250		2(x3+125)
lim to −5		= lim to −5		= lim to −5
	x2+4x−5		x2+4x−5

	2(x+5)(x2−5x+25)		2(x2−5x+25)
		= lim to −5
	(x+5)(x−1)		x−1

Musiałem gdzieś popełnić po drodze błąd, bo to nie ma sensu. Jak zrobić to poprawnie?

gf: Dobra, źle po prostu w pamięci tą 5−tką obracałem podczas ostateczniego obliczania. Wyszło −25

Janek191: x³ + 125 = x³ + 5³ = ( x + 5)*(x² − 5 x + 25)

	2*( x2 − 5 x + 25)
f(x) =
	x −1

więc

	150
lim f(x) =		= − 25
	−6

x→ −5

gf: Jak zabrać się do takiego przykładu?

	1
lim to 0 xsin
	x

Janek191:

	1		1   sin   x
f(x) = x*sin		=
	x		1   x

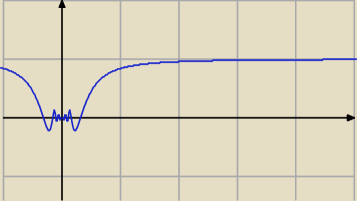
lim f(x) = 1 x→∞

	1
oraz lim f(x) = 0 bo −1 < sin		< 1
	x

x →0

gf: Nie bardzo rozumiem. Nie da się tego zrobić jakimś innym sposobem? //z innej beczki. Mógłby ktoś na szybko sprawdzić, czy dobrze wyszło? Wolframem nie wiem jak sprawdzić ciągłość. http://prntscr.com/ahnhdw