rachunek Metis: P(A')=0,2 P(B')=0,4 P(A'∩B')=0,15 Oblicz P(A∩B) P(A'UB')=P(A')+P(B')− P(A'∩B')

	9
stąd P(A'UB')=
	20

Z praw de Morgana dla zbiorów: P(A'UB')=P(A∩B)' czyli:

	9
P(A∩B)' =
	20

	9
P(A∩B)=1−		=0,55 ?
	20

Eta:

Metis: Witaj Eta Masz może jakieś zadanka tego typu z dopełnieniami ? Przejrzałem to co mam i mam tylko takie Jeśli masz to proszę wrzuć mi je do przećwiczenia

kyrtap: Metis kiedy matura z roz?

Eta: Hej Metis Zadania info ( przejrzałeś? Mam takie ( nie wiem czy są na info( nie chce mi się sprawdzać 1/ A,B ⊂Ω i P(A∩B^')=0,3 i P(A^'∩B)=0,2 wykaż,że P(A∩B)≤,5 2/ A,B⊂Ω i P(A)=0,6 i P(B)=0,8 Wykaż ,że P(A|B)≥0,5 3/ A,B⊂Ω i P(AUB^')=023 i P(A^'UB^")=0,81 Wykaż,że jeśli P(A) <0,21 to P(A^'∩B^')≥0,02 Powodzenia

Metis: 9 maj

Metis: Dziękuje

kyrtap: sporo jeszcze czasu

Metis: Działam

Metis: Losujemy kolejno bez zwracania liczby ze zbioru {1,2,3,4,5,6,7}.Zapisane w kolejności tworzą ciąg 7− wyrazowy. Prawdopodobieństwo, że otrzymany ciąg będzie monotoniczny jest równe: Ciąg wylosowanych liczb będzie monotoniczny tylko wtedy gdy wylosujemy kolejno 1,2,3,4,5,6,7 lub 7,6,5,4,3,2,1 Czyli takich ciągów jest 2. Model : D_l − losowy wybór liczb ze zbioru 7 elementowego bez zwracania Taki wybór utożsamiamy z permutacjami, zatem: Moc Ω=7! A− zdarzenie polegające na ułożeniu ciągu 7 wyrazowego w taki sposób by był monotoniczny Moc A= 2 Na pods. kl. def. prawdopodobieństwa:

	2
P(A)=
	7!

Jest ?

Metis: Z urny zaw. 11 ponumerowanych kul losujemy 3 bez zwracania. Prawdopodobieństwo, że numery wszystkich wylosowanych kul bedą nieparzyste wynosi . D_l− wybór 3 kul z 11 bez zwracania Moc Ω=11*10*9 //losujemy pierwsza − mamy 11 możliwości drugą już 10 trzecią 9 A− zdarzenie w którym numery wylosowanych kul są nieparzyste Czyli mamy do {1,3,5,7,9,11} I nie wiem jaka będzie moc zbioru A

Eta: No to teraz próbna matura zad1/ Wyznacz wszystkie wartości rzeczywiste parametru "m" dla których równanie: 5x²−mx+1=0 ma dwa pierwiastki , których różnica jest równa 1 zad2

	sin2(3x)		cos2(3x)
Rozwiąż równanie:		=4+		dla x∊<−π,π>
	sin2(x(		cos2(x)

zad3 Iloczyn trzech liczb pierwszych jest równy pięciokrotnej sumie tych liczb Wyznacz te liczby zad4 W stożek wpisano kulę. Ze środka tej kuli widać tworzącą stożka pod kątem α. Wyznacz stosunek objętości kuli do objętości stożka zad5 W trójkącie ostrokątnym ABC obrano wewnątrz punkt K, następnie poprowadzono proste równoległe do boków i przechodzące przez K. Z takiego podziału trójkąta otrzymano trzy czworokąty i trzy trójkąty o polach P₁, P₂,P₃. Wykaż ,że pole trójkąta ABC jest równe: (√P₁+√P₂+√P₃)² Powodzenia

Metis: 5. Znam dowód na pamięć

Eta:

Metis: 5. Eta nie pokazuje , to zadanko trafiło mi sie kilka dni temu w moich zadankach, które rozwiązuje i sprawdziłem dowód w odp. Sam nie dałbym rady tego dowieść − teraz wiem, jak to udowodnić, więc może ktoś inny z nim powalczy

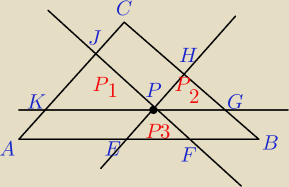
Metis: Do 5.

Metis: Jeśli możesz to zerknij na te moje zadanka wyżej

Metis: Eta w 1) liczę i wychodzi mi ciągle, że nie istnieje takie m. Jaka jest poprawna odp. ?

Metis: Chociaż nie m=√45 v m=−√45

Metis: http://i.imgur.com/pZykeUW.jpg Zgadza się Wzorkami Viete'a też wychodzi.

Metis:

Metis: up