wielomiany
moraw11: ZADANIE 2 (1 PKT)
Dany jest wielomian W(x) = x3 + ax2 + bx − 1, gdzie a i b są liczbami całkowitymi. Zatem
A) Jezeli równanie W(x) = 0 ma pierwiastek wymierny, to a + b = 0.
B) Jezeli równanie W(x) = 0 ma ujemny pierwiastek całkowity, to a = b + 2.
C) Równanie W(x) = 0 moze nie mieć rozwiazań.
D) Równanie W(x) = 0 musi mieć co najmniej 2 rózne pierwiastki.
Prosze o wytłumaczenie zadania
20 mar 12:22
===:
Jeśli ma pierwiastki całkowite ... to sprawdźmy −1 i 1
W(−1)=0=−1+a−b−1 ⇒ a=b+2 czyli założenie B jest prawdziwe
W(1)=0=1+a+b−1 ⇒ a+b=0 czyli założenie A jest prawdziwe
C) to oczywisty fałsz
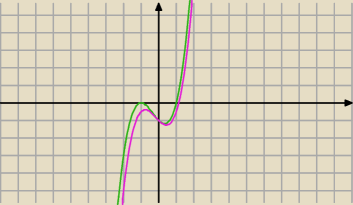
D) to też fałsz. Może mieć ... ale nie musi

20 mar 13:38
 Jeśli ma pierwiastki całkowite ... to sprawdźmy −1 i 1
W(−1)=0=−1+a−b−1 ⇒ a=b+2 czyli założenie B jest prawdziwe
W(1)=0=1+a+b−1 ⇒ a+b=0 czyli założenie A jest prawdziwe
C) to oczywisty fałsz
D) to też fałsz. Może mieć ... ale nie musi
Jeśli ma pierwiastki całkowite ... to sprawdźmy −1 i 1
W(−1)=0=−1+a−b−1 ⇒ a=b+2 czyli założenie B jest prawdziwe
W(1)=0=1+a+b−1 ⇒ a+b=0 czyli założenie A jest prawdziwe
C) to oczywisty fałsz
D) to też fałsz. Może mieć ... ale nie musi 