Równanie z wartościami bezwzględnymi
Slavko: Rozwiąż równanie
|3x−6|−|x
2−4|
Chcę to rozwiązać przedziałami z tym ,że mam problem ponieważ 2 wartość bezwzględna ma 2
pierwiastki z tego jeden taki sam jak w pierwszej. Jak sb tym poradzić


20 mar 10:08
5-latek : Ale to nie jest równanie
20 mar 10:11
Janek191:

20 mar 10:17
Metis: Janek już w gotowości

20 mar 10:18
ICSP: Schemat jest identyczny.
1o x ∊ (− ∞ ; −2]
2o x ∊ ]−2 , 2[
3o x ∊ [2 ; + ∞)
20 mar 10:20
Janek191:
3 I x − 2 I − I ( x −2)*(x + 2) I = 0
3I x − 2 I − I x − 2 I* I x + 2 I = 0
I x − 2 I*( 3 − I x + 2 I) = 0
I x − 2 I = 0 lub I x + 2 I = 3 itd.
20 mar 10:20
zef: jeżeli prawa strona jest równa zero to:
x=3x−6
y=x2−4
I po kolei
x≥0
y≥0
x≥0
y<0
x<0
y≥0
x<0
y<0
20 mar 10:20
zef: No ICSP napisał w skrócie bo u mnie 1 warunek będzie i tak sprzeczny

20 mar 10:21
Slavko: O przepraszam ,zapomniałem przyrównać do zera .Jak bd wyglądał przedział x∊<−2,2)

Bo w tym mam największy problem bo wychodziłoby ,że jedna wartość bezwzględna ma znak dodatni i
ujemny zarazem
20 mar 10:24
Janek191:
Odp.
x = − 5 lub x = 1 lub x = 2
=====================
20 mar 10:26
zef: przedział jest dobry i w tym przedziale oba moduły będą ujemne, sprawdź.
20 mar 10:27
Janek191:
Trzeba trochę pomyśleć !

I a *b I = I a I*I b I
20 mar 10:30
Slavko:
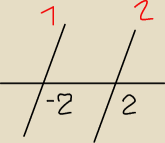
1 to moja prosta y=3x−6 , a 2 to prosta y=3x−6 i prosta y=x
2−4 .I wyraźnie tutaj widać ,że
mają 2 różne znaki
20 mar 10:45
Slavko: Wtedy dla tego przedziału sprawdzam 2 przypadki, tak

20 mar 10:47
Janek191:
@ Slavko:
Jak się już uczepiłeś tych przedziałów, to rób tak, jak podpowiada ICSP:

20 mar 10:53
Slavko: Tak na prawdę tylko w tej metodzie się nie mylę

Tylko mam z tym jednym przedziałem problem

20 mar 10:57
Janek191:
Z którym ?
20 mar 10:57
zef: Zauważ gdzie są znaki "otwarte" i "zamknięte" może wtedy ci się wszystko wyjaśni

20 mar 10:59
Slavko: 1.x ∊ (− ∞ ; −2>
2. x ∊ (−2 , 2>
3. x ∊ (2 ; + ∞)
Tak sb to rozpisałem
20 mar 11:04
Slavko: Już wszystko dla mnie jasne ,dziękuje Wam za pomoc

20 mar 11:05





 Bo w tym mam największy problem bo wychodziłoby ,że jedna wartość bezwzględna ma znak dodatni i
ujemny zarazem
Bo w tym mam największy problem bo wychodziłoby ,że jedna wartość bezwzględna ma znak dodatni i
ujemny zarazem
 I a *b I = I a I*I b I
I a *b I = I a I*I b I
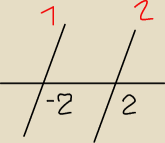 1 to moja prosta y=3x−6 , a 2 to prosta y=3x−6 i prosta y=x2−4 .I wyraźnie tutaj widać ,że
mają 2 różne znaki
1 to moja prosta y=3x−6 , a 2 to prosta y=3x−6 i prosta y=x2−4 .I wyraźnie tutaj widać ,że
mają 2 różne znaki


 Tylko mam z tym jednym przedziałem problem
Tylko mam z tym jednym przedziałem problem


