stereo hegel: dany jest ostroslup prawidłowy trójkątny ABCS O podstawie ABC i wysokości SO . Objętość ostroslupa wynosi 96√3 . Punkty E, P,Q,R są odpowiednio środkami odcinków BC,SO,SE, i SC. Objętość ostroslupa PQRS jest równa

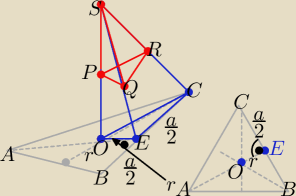
Eta: Trójkąty OEC i PQR są prostokątne |∡OEC|=|∡PQR|=90^o Cały ostrosłup składa się z sześciu przystających ostrosłupów do OECS

	1		1
V(OECS)=		V(ABCS)=		*96√3=16√3
	6		6

i ostrosłup OECS jest podobny do ostrosłupa PQRS w skali k=2 to ich objętość jest w stosunku k³=8

	1
zatem V(PQRS)=		*16√3=2√3 [j3]]
	8

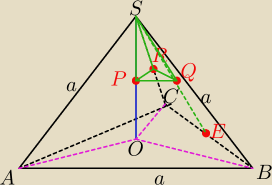CienkiBolek: Jeżeli wyznaczysz H=SO zależne od „a" to wyliczysz „a" z objętości dużego ostrosłupa A potem proporcje gonią proporcje aż do wyznaczenia PQ PR i RQ. PS to połowa SO. No i potem......... objętość ostrosłupa PQRS Good luck