geometria analityczna Ireneusz: Dany jest trójkąt ABC, gdzie punkt A jest początkiem układu współrzędnych, a punkty B i C są punktami przecięcia prostej l: 2x – y – 8 = 0 z osiami układu współrzędnych. Prosta k: y = ax dzieli ten trójkąt na dwa trójkąty, których stosunek pól jest równy 2:3. Wyznacz wartość a. Rozpatrz wszystkie przypadki.

Metis: Współrzędne policzone ?

Ireneusz: nic.. tylko tyle..

Ireneusz: domyślam się, że punkty B i C to (x;2x−8) Ale to chyba oczywiste..

Metis: No tak, mogłem się tego spodziewać... Czy ty policzyłeś współrzędne ?

Ireneusz: nie

===:

Metis: To licz. Wszystko podane na widelcu.

Ireneusz: aaaa dobra xD czytać nie umiem... Nie przeczytałem, że punty A i B leżą na osiach.. dzięki

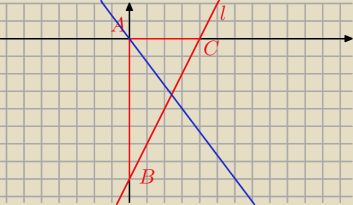
Janek191: I przypadek y = a x y = 2 x − 8 więc a x = 2 x − 8 ( a − 2) x = − 8

	−8		8
x =		=
	a − 2		2 − a

	8 a
y = a x =
	2 − a

	8		8 a
P = (		,		)
	2 − a		2 − a

	8a		8a		16a
P1 = 0,5*I AC I*I		I = I 2*		I = I		I
	2 − a		2 −a		2 −a

	8		8		32
P2 =0,5* I AB I*		= 4*		=
	2 − a		2 −a		2 −a

	16a		2 − a		2		4
P1 : P2 = I		I*		= I 0,5 a I =		⇒ a =− −
	2 −a		32		3		3

	4
y = −		x
	3

===========