a Benny:

	3
x∊<		π; 2π>
	2

√3sin2x+3cos2x=0 cos2x≠0 √3sin2x+3cos2x=0 /:cos2x √3tg2x+3=0 tg2x=−√3

	2
2x=		π+kπ
	3

	1		kπ
x=		π+
	3		2

	11
x=		π
	6

Godzio: Wygląda ok

Benny:

	1
max. f(x)=		(1+3cos2x)
	6

0≤cos²x≤1 /*3 0≤3cos²x≤3 /+1

	1
1≤1+3cos2x≤4 /*
	6

1		1		2
	≤		(1+3cos2x)≤
6		6		3

	2
max. f(x)=
	3

Benny:

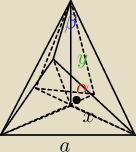
	1
(		a)2=y2+y2−2y2cosβ
	2

1   a 3
	=cosα
y

	a
y=
	3cosα

1
	a2=2*y2(1−cosβ)
4

1		a2
	a2=2*		(1−cosβ) /:a2
4		9cos2α

1		2
	=		(1−cosβ)
4		9cos2α

9cos2α
	=1−cosβ
8

	9cos2α
cosβ=1−
	8

	8−9cos2α
cosβ=
	8

Odpowiedź jest inna, ale nie widzę, żebym gdzieś zrobił błąd. Polecenie to: W ostrosłupie prawidłowym trójkątnym kąt między ścianą boczną a podstawą jest równy α.Oblicz cosinus kąta między ścianami bocznymi.

Jack:

	5
odp. =		tg2 α ?
	2

Jack: http://puu.sh/mNhew/3bb4cd9d8d.png http://puu.sh/mNjom/6d888e1ddb.png jesli tak −>ok jesli nie−>to nwm

Jack: a blad masz w zaznaczeniu kata (tak mi sie wydaje)...kat miedzy scianami bocznymi jest w innym miejscu

Jack: tam mam blad oczywiscie... http://puu.sh/mS770/d5715dbac5.png poprawny wynik : http://puu.sh/mS88W/c168caa6c9.png

1 − 3 cos2α
2

Jack: i zle wyciagniecie przed nawias i wgl...ale te poczatkowe rownania sa ok, tylko potem sie w obliczeniach "zarabalem" odp. po poprawkach powinna sie zgadzac...

Benny: Nawet nie widzę co tam jest liczone w ogóle. Ogarnąłem już błąd u siebie. Dzięki i tak

Jack: sorki, ze tak chaotycznie

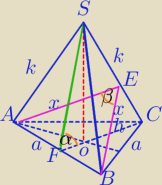Mila: W ostrosłupie prawidłowym trójkątnym kąt między ścianą boczną a podstawą jest równy α. Oblicz cosinus kąta między ścianami bocznymi.

	1		a√3
|FO|=		h=
	3		6

WΔSOF:

	|OF|
cosα=
	|FS|

	|OF|
|FS|=
	cosα

	h
|FS|=
	3cosα

	H		h*tgα
tgα=		⇔H=
	1   h 3		3

	1		h		a*h
PΔABS=		*a*		=
	2		3cosα		6cosα

WΔSOC:

	2
k2=H2+(		h)2
	3

	h2*tg2α		4		h2		h2		sin2α+4cos2α
k2=		+		h2=		*(tg2α+4)=		*
	9		9		9		9		cos2α

	h√1+3cos2α
k=
	3cosα

	1		1		h√1+3cos2α
PΔBCS=		*x*k=		x*
	2		2		3cosα

1		h√1+3cos2α		a*h
	x*		=		⇔
2		3cosα		6cosα

x*√1+3cos²α=a

	a
x=
	√1+3cos2α

a²=x²+x²−2x²cosβ a²=2x²*(1−cosβ)

	2a2
a2=		*(1−cosβ)
	1+3cos2α

	1−3cos2α
cosβ=
	2

=============

Jack: liczylem bardzo podobnie jak [F[Mila]

Benny: Dziękuje Milu nie dość, że źle zaznaczyłem kąt to na dodatek napisałem, że ten mały odcinek to trzecia cześć boku, a nie wysokości

Mila: