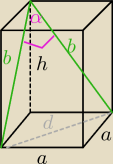
 Dany jest prostopadłościan o podstawie kwadratowej i wysokości h
a) wyznacz pole przekroju prostopadłościanu płaszczyzną przechodzącą przez przekątne sąsiednich
ścian bocznych wychodzące z jednego wierzchołka, jeśli wiadomo, że kąt między nimi ma miarę α
b) Wyznacz α, tak aby pole przekroju prostopadłościanu płaszczyzną przechodzącą przez przekątne
sąsiednich ścian bocznych wychodzące z jednego wierzchołka było równe P= h22
d= a√2
na razie obliczyłam tyle, że
b=h√cosα
a= h √1−cosαcosα
i co dalej?
Dany jest prostopadłościan o podstawie kwadratowej i wysokości h
a) wyznacz pole przekroju prostopadłościanu płaszczyzną przechodzącą przez przekątne sąsiednich
ścian bocznych wychodzące z jednego wierzchołka, jeśli wiadomo, że kąt między nimi ma miarę α
b) Wyznacz α, tak aby pole przekroju prostopadłościanu płaszczyzną przechodzącą przez przekątne
sąsiednich ścian bocznych wychodzące z jednego wierzchołka było równe P= h22
d= a√2
na razie obliczyłam tyle, że
b=h√cosα
a= h √1−cosαcosα
i co dalej?

| 1 | ||
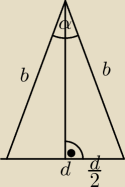
a) Dane: α, h P=? P = | *b2sinα | |
| 2 |
| d/2 | α | |||
= sin | ||||
| b | 2 |
| α | |||||||||
= sin | ||||||||||
| b | 2 |
| α | ||
a√2 = 2bsin | ||
| 2 |
| 2b | α | α | ||||
a = | sin | = b√2sin | ||||
| √2 | 2 | 2 |
| α | ||
Czyli po podstawieniu: b2 = h2 + 2b2sin2 | ||
| 2 |
| α | ||
b2 − 2b2sin2 | = h2 | |
| 2 |
| α | ||
b2(1 − 2sin2 | ) = h2 | |
| 2 |
| h2 | |||||||||||
b2 = | |||||||||||
|
| 1 | h2 | h2sin2α | ||||||||||||||||||||||
Zatem: P = | * | *sinα = | ||||||||||||||||||||||
| 2 |
|
|
| h2 | ||
b) Dane: h, P= | α=? | |
| 2 |
| 1 | ||
P= | b2sinα | |
| 2 |
| 1 | h2 | |||
Czyli | b2sinα = | /*2 | ||
| 2 | 2 |
| h2 | ||
b2sinα = h2 ⇒ sinα = | ||
| b2 |
| a2 | ||
h2 + a2 = | ||
| 1 − cosα |
| a2 | ||
h2 = | − a2 | |
| 1−cosα |
| 1 | ||
a2( | − 1) = h2 | |
| 1−cosα |
| 1−1+cosα | ||
a2 * | = h2 | |
| 1−c0sα |
| cosα | h2(1−cosα) | |||
a2 * | = h2 ⇒ a2 = | |||
| 1−cosα | cosα |
| a2 |
| |||||||||
Wtedy b2 = | = | = | ||||||||
| 1−cosα | 1−cosα |
| h2(1−cosα) | 1 | h2 | ||||
= | * | = | ||||
| cosα | 1−cosα | cosα |
| h2 | cosα | |||||||||
Zatem: sinα = | = h2* | = cosα | ||||||||
| h2 |
| a2 | ||
a2 = b2(1−cosα) ⇒ b2 = | ||
| 1−cosα |
 muszę na spokojnie przeanalizować
muszę na spokojnie przeanalizować

 Gdy coś nie będzie jasne, to pisz.
Gdy coś nie będzie jasne, to pisz.
 Mogę podać swoje rozwiązanie tego zad ?
Mogę podać swoje rozwiązanie tego zad ?  Widzę ile się napracowałaś ..... mam nieco krótszy sposób rozwiązania
Widzę ile się napracowałaś ..... mam nieco krótszy sposób rozwiązania 

 wykorzystuję Twoje oznaczenia:
P= 12b2*sinα
ze wzoru cosinusów: w tym przekroju:
d2 = b2 +b2 −2b2*cosα i d2 = 2a2
wykorzystuję Twoje oznaczenia:
P= 12b2*sinα
ze wzoru cosinusów: w tym przekroju:
d2 = b2 +b2 −2b2*cosα i d2 = 2a2
| a2 | ||
2a2 = 2b2( 1 −cosα) => b2 = | ||
| 1−cosα |
| a2 | ||
b2 = H2 +a2 => | − a2 = H2
| |
| 1−cosα |
| a2( 1 −1 +cosα) | ||
to: | = H2
| |
| 1−cosα |
| a2*cosα | ||
= H2
| ||
| 1−cosα |
| H2( 1−cosα) | ||
to a2 = | ||
| cosα |
| H2(1−cosα) | H2 | |||
więc b2= | = | |||
| cosα(1−cosα) | cosα |
| h2 | h2*tgα | |||
więc P= 12 | *sinα= | |||
| cosα | 2 |
| H2 | H2 | |||
w b) | = | *tgα
| ||
| 2 | 2 |

 ja właśnie obliczyłam a i b sposobem Ety, tylko potem pole mi wcale a wcale nie chciało
wyść
ja właśnie obliczyłam a i b sposobem Ety, tylko potem pole mi wcale a wcale nie chciało
wyść Teraz mam już 2 sposoby rozwiązania
Teraz mam już 2 sposoby rozwiązania Będę pamiętała na maturze (mam nadzieję
Będę pamiętała na maturze (mam nadzieję  )
)
 Oczywiście Twoje rozwiązanie jest jak najbardziej poprawne
Oczywiście Twoje rozwiązanie jest jak najbardziej poprawne ale gdybyś w polu podanym przez Ciebie ;
ale gdybyś w polu podanym przez Ciebie ;
| H2 *sinα | ||
P= | ||
| 1 − 2sin2α2 |
| H2*sinα | h2*sinα | H2 | ||||
zatem: P= | = | = | *tgα
| |||
| 1 −1 +cosα | cosα | 2 |
 Pozdrawiam
Pozdrawiam 




 ?
? 


 Oczywiście
Oczywiście  Tylko przydało by się , by młodzież wrzuciła trochę zadań
Tylko przydało by się , by młodzież wrzuciła trochę zadań 

 bo co będziemy robić
bo co będziemy robić


 Młodzi ...... pamiętajcie o tym
Młodzi ...... pamiętajcie o tym 


 !
!





 ......... balujesz jutro
......... balujesz jutro  ?
?






 a w niedzielę to juz nie pomagam ( a będzie pewnie "wysyp"
a w niedzielę to juz nie pomagam ( a będzie pewnie "wysyp" 


 m€ R \{0}
3) xw >0 .... m>0
4) f(1) >0 bo ramiona paraboli do góry z warunku 3)
wyszła mi odp: m€ ( 0,1)
m€ R \{0}
3) xw >0 .... m>0
4) f(1) >0 bo ramiona paraboli do góry z warunku 3)
wyszła mi odp: m€ ( 0,1)

 ale to później wrzucę
ale to później wrzucę 