dlugosc wektora shagaru: Punkty A (2,0), B (1,3), C (−5,1) sa wierzcholkami trojkata. Punkt D nalezy do boku BC, zas odcinek AD zawiera sie w dwusiecznej kata CAB. Wyznacz dlugosc wektora AD

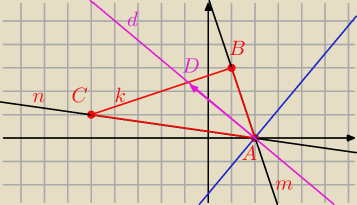
Janek191: A =( 2, 0) B = ( 1,3) C = ( − 5, 1) Prosta AB

	3 −0
a1 =		= − 3
	1 −2

y = − 3 x + b₁ 0 = −3*2 + b₁ ⇒ b₁ = 6 y = − 3 x + 6 m : 3 x + y − 6 = 0 ========== Prosta AC

	1 − 0		1
a2 =		= −
	− 5 − 2		7

	1
y = −		x + b2
	7

	1		2
0 = −		*2 + b2 ⇒ b2 =
	7		7

	1		2
y = −		x +
	7		7

7 y = − x + 2 n : x + 7 y − 2 = 0 ============= Szukanie dwusiecznej ∡ CAB

I 3 x + y − 6 I		I x + 7 y − 2 I
	=
√10		√50

Otrzymujemy równanie dwusiecznej:

	− ( 3 √5 + 1) x + 6√5 + 2
d : y =
	7 +√5

Prosta BC

	1 − 3		1
a3 =		=
	− 5 − 1		3

	1
y =		x + b3
	3

	1		2
3 =		+ b3 ⇒ b3 = 2
	3		3

	1		8
k : y =		x +
	3		3

================== Punkt D jest punktem wspólnym prostych: k i d Obliczamy wektor AD i jego długość I AD I..

Aga1.: Masz odp. do tego zadania? Robiłam nieco inaczej. Nie wiem, czy nie pomyliłam się w obliczeniach, bo wynik nieciekawy.