 1.Podstawą ostrosłupa jest trójkąt równoboczny. Wysokość ostrosłupa wychodzi ze środka krawędzi
podstawy. Najdłuższa krawędź boczna ma długość √ i tworzy z płaszczyzną podstawy ostrosłupa
kąt 45o. Oblicz objętość ostrosłupa.
2.Podstawa ostrosłupa jest trójkąt równoramienny prostokątny. Wysokość wychodzi ze środka
przeciwprostokątnej. Uzasadnij że każda z krawędzi bocznych jest nachylona do płaszczyzny
podstawy pod takim samym kątem
3.Podstawą ostrosłupa jest trójkąt równoramienny. Każda ściana boczna tworzy z płaszczyzną
podstawy taki sam kąt. Uzasadnij że wysokość wychodzi ze środka koła wpisanego w podstawę.
1.Podstawą ostrosłupa jest trójkąt równoboczny. Wysokość ostrosłupa wychodzi ze środka krawędzi
podstawy. Najdłuższa krawędź boczna ma długość √ i tworzy z płaszczyzną podstawy ostrosłupa
kąt 45o. Oblicz objętość ostrosłupa.
2.Podstawa ostrosłupa jest trójkąt równoramienny prostokątny. Wysokość wychodzi ze środka
przeciwprostokątnej. Uzasadnij że każda z krawędzi bocznych jest nachylona do płaszczyzny
podstawy pod takim samym kątem
3.Podstawą ostrosłupa jest trójkąt równoramienny. Każda ściana boczna tworzy z płaszczyzną
podstawy taki sam kąt. Uzasadnij że wysokość wychodzi ze środka koła wpisanego w podstawę.

 l = ? nie można odczytać z zadania
l = ? nie można odczytać z zadania
| H | √2 | ||
= sin 45o = | |||
| l | 2 |
| l√2 | ||
H = | ||
| 2 |
| hp | √2 | ||
= cos45o = | |||
| l | 2 |
| l√2 | ||
hp = | ||
| 2 |
| 2 | ||
a = | hp√3 = | |
| 3 |
| a2√3 | ||
V = | *H = | |
| 12 |
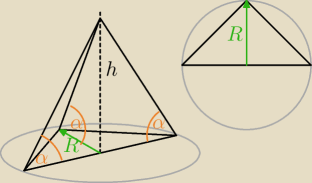
| h | ||
tgα = | ||
| R |
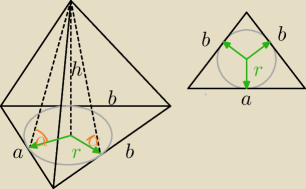
| h | |
= tgα | |
| r |
