pomoże ktoś?to znaczy sprawdzi czy mam dobrze Justyna: Dana jest funkcja f(X)=2x²−4x−6 a)oblicz wyróżnik,miejsca zerowe,współrzędne wierzchołka i narysuj jej wykres b)podaj dziedzinę,zbiór wartości,wartości ekstremalne,przedziały monotoniczności mam tak: f(X)=2x²−4x−6 a= 2 b=−4 c=−6 Δ=b²−4ac Δ=(−4)²−4*2*(−6) Δ=16−8*(−6) Δ=16+48 Δ=64>0 ma dwa miejsca zerowe x₁=obliczyłam że to będzie −1 a x₂=+1 dobrze? WSPÓŁRZĘDNE WIERZCHOŁKA OBLICZYŁAM ŻE: p=1 a q=8

pytajnik123: x₁=^−b−√Δ_2a x₂=^−b+√Δ_2a X_w=^−b_2a Y_w=^−Δ_4a

pytajnik123: x₂ i y_w tak średnio chyba

Justyna: x₁=−1 x₂=3

pytajnik123: Tak, jeszcze q=−8

Justyna: Super tylko jak ma teraz podac dziedzine ? zbior itp ?

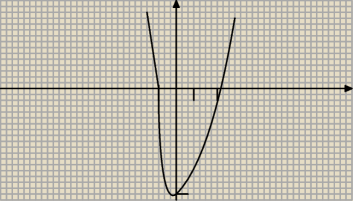
Justyna: tak mniej wiecej D=<−1;3> ZW=(+∞...I TU NIE WIEM Wartości ekstremalne=ymax=∞ ymin=−8 Przedział monotoniczności:monotoniczna przedziałami malejąca(−∞;−8> rosnąca<−8;3>

Janek191: Dziedziną każdej funkcji kwadratowej jest ℛ.

Janek191: Dla a > 0 jest ZW = < q , + ∞ )

Justyna: Teraz mam kolejne zadanie : Zapisz funkcje f(x)=−x²−6x−8 w postaci iloczynowej a=−1 b=−6 c=−8 Δ=b²−4ac Δ=36²−4*(−1)*(−8) Δ=36−32 Δ=4 x₁=2 x₂=4

Janek191: Dla a > 0 funkcja kwadratowa maleje , gdy x < p , a rośnie , gdy x > p.

Arek: źle obliczyłaś x₂ a także q, ponieważ

	4+8		12
x2=		=		=3
	4		4

a twoje q wynosi

	−8
q=		=−1
	8

Aby odczytać monotoniczność funkcji oraz zbiór wartości funkcji najłatwiej jest narysować wykres na podstawie danych które posiadasz,a następnie odczytać z niego potrzebne dane. Zbiór wartośći funkcji odczytujemy z osi OY, w tym przypadku ramiona wykresu pójdą do góry ponieważ w wzorze funkcji przed naszym a czyli 2x² nie stoi minus.

Janek191: Δ − początek źle 6² , a nie 36² a = − 1 y = a*(x − x₁)*(x − x₂)

Janek191: Oba pierwiastki ( miejsca zerowe) źle policzone.

Arek: Co do drugiego zadania wystarczy popatrzeć do tablic matematycznych gdzie napisany jest wzór na postać iloczynową: f(x)=a(x−x₁)(x−x₂) podłóż do wzoru i bo zadaniu

Arek: oczywiście najpierw trzeba obliczyć x₁ i x₂ z Δ

Justyna: co do drugiego zadania Janek191 przeciez b² czyli 6*6=36 to jak mam zle obliczone

Arek: chodzi mu o błąd w zapisie ponieważ napisałaś Δ=36²−4*(−1)*(−8) a być powinno Δ=6²−4*(−1)*(−8)

Justyna: aha no tak ale obliczone jest dobrze?

Arek: co do obliczeń w drugim x₁ i x₂ są obliczone źle, wydaje mi się że nie wzięłaś pod uwagę minusa przy a, które rowna się a=−1 a nie 1

Justyna: Δ=4

Janek191: Tak Oblicz x₁ i x₂.

Justyna: x₁ bedzie −2 a x₂ bedzie −4

Arek: tak,tak Δ jest okay tylko wydaje mi się że zapomniałaś tego minusa przy a

Arek: i teraz jest dobrze podłóż do wzoru funkcji iloczynowej f(x)=a(x−x1)(x−x2) i zadanie zrobione

Justyna:

	−b − √Δ
x1=
	2a

	−6 − √4
x1=
	2*(−1)

x₁=U{ 6 − 2 } { 2 } x₁=U{ 4 } { −2 } x₁=−2

Justyna: i na podobe x₂

Justyna: y=−1(x+2)(x+4)

Justyna: czy zamiast plusow minusy ?

Justyna: mam jeszcze 3 zadania tylko czy ma ktos ochote mi to sprwdzic

Justyna: mam jeszcze 3 zadania tylko czy ma ktos ochote mi to sprwdzic

Janek191:

	6 − 2		6 +2
x1 =		= −2 x2 =		= − 4
	−2		−2

Janek191: y = − ( x + 2)*( x + 4) ================

Justyna: zad3 zapisz funkcje f(x)=−4²+8x−6 w postaci kanonicznej

Arek: Tak teraz jest dobrze, tylko że mogłaś napisać poprostu: y= −(x+2)(x+4) nie trzeba pisać 1 przed nawiasem, chyba że byłaby to większa liczba to wtedy musisz ją napisać. Dlaczego nie dawaj zobaczymy co tam masz

Justyna: czyli juz teraz dobrze

Janek191: Przepisz funkcję − z.3 Brak x

Justyna: −4x²−8x−6 Δ=b²−4ac Δ=8²−4*(−4)*(−6) Δ=64−96 Δ=−32

Janek191: f(x) = − 4 x² − 8 x − 6 O 19.39 była inna funkcja

Justyna: a=−4 b=8 c=−6

Justyna: Janek191 tam nie wpisalm x teraz ta jest ok

Janek191: Δ = 64 − 4*(−4)*(−6) = 64 − 96 < 0 − brak miejsc zerowych Nie ma postaci iloczynowej.

Justyna:

	−b
p=
	2a

	−8 − 2
p=
	2*(−4)

	−8
p=
	−8

p=1

	−Δ
q=
	4a

	−32
q=
	4*(−4)

	−32
q=
	−16

q=−2

Janek191: y = − 4 x² + 8 x − 6

Justyna: i tak mam to narysowac? a ja mam tak y=−4(x−1)²−2

Arek: delta jest okay tylko że tak samo jak w poprzednim zadaniu przy obliczaniu p i q zapomniałaś o minusach dwa minusy dają nam plus więc −b= 8 a nie −8

Janek191: A miała być kanoniczna

	−b		−8
p =		=		= 1
	2a		− 8

q = f(p) = f(1) = − 4*1² + 8*1 − 6 = − 4 + 8 − 6 = − 2 W = ( p, q ) = ( 1, − 2) a = − 4 więc y = − 4*( x − 1)² − 2 ==============

Janek191: Wykres masz narysowany − 19.51

Arek: jeżeli chcesz zamienić na postać kanoniczną to podkładasz do wzoru na postać kanoniczną który wygląda następująco: f(x)= a(x − p)² + q

Justyna: te a=− to skad ? czyli obliczenia mam dobre ?

Justyna: te a=−4 to skad

Janek191: Napisałaś y = − 4 x² + 8 x − 6 a = − 4 b = 8 c = − 6

Arek: szkoda że na tym forum nie da się używać cytatów, o które a=− ci chodzi ?

Arek: Hah no chyba że tak to wszystko dobrze

Janek191: Tam była pomyłka − 19.50 Ma być

	− 8		−8
p =		=		= 1
	2*(−4)		−8

Justyna: a no tak za duzo juz tej matematyki juz nie mysle

Justyna: no tak mam napisane

Janek191: Dawaj następne

Justyna: rozwiąż równanie (4x−5)²=−40+34

Janek191: Lewa oblicz. Prawą popraw.

Justyna: tylko ze na lekcjach mialam ze wszystko trzeba przeniesc na prawa itd i pozniej pierwiastkowac i nie wiem jak to zrobic czy x na lewo liczy na prawo

Janek191: Do lewej wzór: (a − b)² = a² − 2 a*b + b²

Janek191: Źle jest przepisane równanie,bo po prawej stronie jest liczba ujemna.

Justyna: mam tak : (4x−5)²=−40+34 16x²−40x+25=−40x+34 16x²−40x+40x=34−25 16x²−9=0

Janek191: Może miało być ( 4 x − 5)² = − 40 x + 34 ?

Justyna: no takie dostalam zadania na prace kontrolna i tam jest −40x+34

Janek191: Pisz porządnie − piszesz raz bez iksa, niżej z iksem !

Justyna: no tak napisalam −20:05

Justyna: boze prepraszam faktycznie tam mial byc x

Janek191: 16 x² − 9 = 0 (4 x)² − 3² = 0 ( 4 x − 3)*( 4 x + 3) = 0 4 x = 3 lub 4 x = − 3

	3		3
x =		lub x = −
	4		4

======================== II sposób: 16 x² − 9 = 0 16 x² = 9 / : 16

	9
x2 =
	16

	3		3
x = −		lub x =
	4		4

Justyna: 16x²−40x+25=−40x+34 16x²−40x+25+40−34 16x²−9=0 jest to rownanie kwadratowe niewiadome na lewa wiadome na prawa i pierwiastkujemy 16x²=9/:16 sprawdzamy teraz cy rownanie jest prawdziwe

	9
x2=		(jest na plusie) wiec rownanie jest prawdziwe i pierwiastkujemy
	16

	9
√x2=√
	16

	3		3
x2=		lub x1=−
	4		4

tak sobie napisalam

Justyna: i ostatnie zad.5 (2x−8)(3x−4)=32−16x

Justyna: ale tu juz naprawde nie wiem jak zrobic

Justyna: cos zaczelam 6x²−8x−24−32=32−16x

pytajnik123 : Wymnazasz nawiasy wszystko na jedną stronę i liczysz

Justyna: 6x²−8x−24x−32=32−16x 6x²−8x−24x−32+32−16x i co dalej ?

Justyna: chyba juz wszyscy spia

Janek191: (2 x − 8)*( 3 x − 4) = 32 − 16 x 6 x² − 8 x − 24 x + 32 = 32 − 16 x 6 x² − 16 x = 0 2x*( 3 x − 8) = 0 x = 0 lub 3 x − 8 = 0

	8
x = 0 lub x =
	3

===============

Justyna: Dziekuje bardzo