Zestaw 2 ćwiczeniowy Kamil: Wyznacz dziedzinę , uprość wzór ,a następnie naszkicuj wykres funkcji f

	x2+x
a) f(x) =
	x

	x2−4
b) f(x) =
	x+2

	4x2−9
c) f(x) =
	1,5−x

Rozwiązania w pierwszym hyba wyjdzie tak Df E R − {0}

	x(x2+1)
f(x) =		= x+1
	x

to są powtórzenia

Kamil:

	x(x+1)
sorry chyba błąd f(x) =		=x+1
	x

Kamil: umie ktoś ?

kochanus (z komorki): W drugim zauwaz ze x²−4 =(x−2)(x+2) W trzecim wyciagasz 4 przed nawias i zauwaz ze 1.25 = (1.5)²

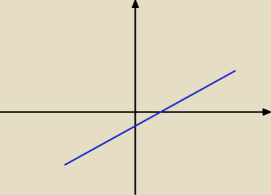
Kamil: spróbowałem rozwiązać też samemu i zrobiłem dwa punkty b) na dwa sposoby i c) na jeden no i nie wiem który sposób jest poprawny zacznę od b) bo a) jest łatwy. b) To jest podpunkt b Przykład 1

	(x−2)(x+2)
y =		= x−2 Df∊R{−2}
	x+2

Przykład 2

x2−4
x+2

Df: x+2≠0 x≠−2 Df: x∊R {−2} jeszcze c), którego nie zrozumiałem ja robię tak Przykład 2

	4x2−2
f(x) =
	1,5−x

	2(x − 2)
y=		= 2 no i tego nie rozumiem.
	1,5 − x

Df: 1,5 − x ≠ 0 x ≠ − 1,5 Df: x ∊ R { − 1,5} Czy ja to dobrze robię

Kamil: a sorry jeszcze ciąg dalszy do Przykład 1

	x−2
y =		= − 2
	x+2

Kamil: sorka Przykład 2