Pochodne funkcji
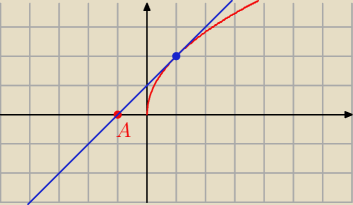
Uneur: Wyznacz rownanie stycznej do wykresu funkcji f(x)=2√x,przechodzacej przez punkt A(−1,0).
17 mar 20:41
Janek191:
f(x) = 2
√x , x ≥ 0
| | 1 | | 1 | |
f '(x) = 2* |
| = |
| |
| | 2 √x | | √x | |
y = a x + b A = (−1, 0)
0 = − a + b ⇒ b = a
y = a x + a
oraz
2
√x = a x + a
4 x = a
2 x
2 + 2 a
2 x + a
2
a
2 x
2 + (2 a
2 + 4) x + a
2 = 0
Δ = 4 a
4 + 16 a
2 + 16 − 4*a
2*a
2 = 16 a
2 + 16 = 0 ⇔ a = 1 lub a = − 1
y = x + 1
=======
17 mar 20:51
===:
Dziedzina ...
równanie pęku prostych przez A
y=a(x+1)
Styczna ma jeden punkt wspólny z krzywą
2√x=a(x+1) ⇒ ax−2√x+a=0
i rozwiązuj
17 mar 20:54
Uneur: Bardzo dziekuje.
17 mar 20:56
Uneur: Janek191 a w 3 linijce od konca nie powinno byc a2x2+(2a2−4)x+a2=0? Przenosisz stronami 4x
wiec zmieniasz znak
17 mar 21:05
Janek191:
Powinno
17 mar 21:09