Planimetria michal: 1. Podstawy trapezu równoramiennego mają długość 6√2 oraz 8√2, a przekątne tego trapezu są prostopadłe. Oblicz pole i obwód tego trapezu. 2.Pole rombu jest równe 15, długość okręgu wpisanego w ten romb jest równa n√5. Oblicz obwód tego rombu. 3.W trapez równoramienny o kącie ostrym 30 stopni wpisano okrąg o promieniu 1,5. Oblicz długości podstaw tego trapezu. 4. Różnica między promieniem okręgu opisanego na kwadracie, a promieniem okręgu wpisanego w ten kwadrat jest równa 3. Oblicz pole tego kwadratu. Z góry dziękuję za pomoc, ponieważ nie mam pojęcia jak to rozwiązać

Janek191: z.1 h = y + x = 0,5 a + 0,5 b = 4√2 + 3√2 = 7 √2 P = h² = 49*2 = 98 [j²] c² = x² + y² = 32 + 18 = 50 = 25*2 c = 5√2 Obwód L = a + b +2 c = 8√2 + 6√2 + 10√2 = 24√2 ==================================== II sposób pole P =√2 x* √2y + x² + y² = 2*3√2*4√2 + 18 + 32 = = 48 + 50 = 98

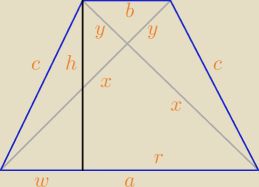Godzio: Wszystko przeliczone na literkach, wstawiaj, licz, myśl x² + x² = a² 2x² = a²

	a2
x2 =
	2

	a
x =
	√2

	b
y =
	√2

	a − b
w =
	2

	a − b		a + b
r = a − w = a −		=
	2		2

h² + r² = (x + y)²

	a + b		a + b
h2 + (		)2 = (		)2
	2		√2

	(a + b)2		(a + b)2
h2 =		−
	2		4

	(a + b)2
h2 =
	4

	a + b
h =
	2

	a + b		a + b
P =		* h = (		)2
	2		2

h² + w² = c²

	a + b		a − b
(		)2 + (		)2 = c2
	2		2

a2 + b2
	= c2
2

	√a2 + b2
c =		= U{√2a2 +2b2{2}
	√2

Obw = 2c + a + b = √2a² + 2b² + a + b

Janek191: Pomyłka w obwodzie c² = (√2 x)² + (√2y)² = 2 x² + 2y² = 2*18 + 2*32 = 36 + 64 = 100 c = 10 L = a + b + 2 c = 8√2 + 6√2 + 20 = 20 + 14 √2 =====================================

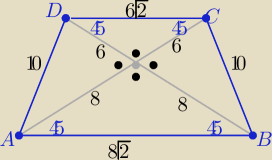Eta: L(ABCD)= 20+14√2 [j]

Eta: Godzio .... jestem w