Wyznacz równanie prostej do której należy punkt P(1,-1) i takiej, że odleglość p Anastazja: Wyznacz równanie prostej do której należy punkt P(1,−1) i takiej, że odleglość punktu Q(8,−2) od tej prostej wynosi 5.

5-latek :

	|Ax0+By0+C|
d=
	√A2+B2

Anastazja: wiem, podstawilam to ale wychodzi mi coś dziwnego :'(

===: równanie pęku prostych przez P y+1=a(x−1) ⇒ ax−y−a−1=0

	|8a+2−a−1|
5=		⇒ 5√a2+1=|7a+1|
	√a2+1

25a²+25=49a²+14a+1 ⇒ 24a²+14a−24=0 12a²+7a−12=0 itd

	4		1		3		7
y=−		x+		lub y=		x−
	3		3		4		4

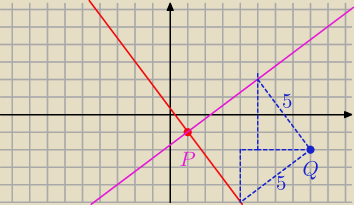
Janek191: P = ( 1, −1) y = a x + b − 1 = a + b ⇒ b = − 1 − a y = a x − 1 − a a x − y − 1 − a = 0 Q = ( 8 , − 2) d = 5

I 8 a +2 −1 − a I
	= 5
√a2 + 1

I 7 a + 1 I = 5 √a² + 1 49 a² + 14 a + 1 = 25 a² + 25 24 a² + 14 a − 24 = 0 / : 2 12 a² + 7 a − 12 = 0 Δ = 49 − 4*12*(−12) = 49 + 576 =625 √Δ = 25

	− 7 − 25		32		4		18		3
a =		= −		= −		lub a =		=
	24		24		3		24		4

	1		3		7
b = − 1 + U4}{3} =		lub b = − 1 −		= −
	3		4		4

Odp.

	4		1		3		7
y = −		x +		lub y =		x −
	3		3		4		4

Anastazja: ślicznie dziękuję, wszystko już rozumiem

===: Jasiek się napracował