Proszę o wskazówkę.
Pirat: Proszę o wskazówkę.
Rożek ma kształt odwróconego stożka o promieniu podstawy 2 dm i wysokości
3 dm. Na jaką wysokość należy nalać wody do rożka,aby wypełniała ona 1/8 objętości rożka?
16 mar 18:55
Metis: Pomyśl

16 mar 18:56
ziaom: nie pomoge
16 mar 18:57
Pirat: przeciąłem płaszczyzną i zrobiłem z trójkątów podobnych, wyszło mi że h =3/2 dobrze?
16 mar 19:31
5-latek :
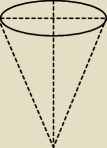
16 mar 19:32
Metis: 
V=1/3P
p* H − w czym problem?
16 mar 19:34
Pirat: no to zrobiłem tak zaznaczyłem na rysunku ten trójkąt który przy obrocie daje 1/8V tego stożka.
zrobiłem z podobnych że r/2=h/3 => h=3r/2 i potem podstawiłem do wzorku który sobie wcześniej
policzyłem.
16 mar 19:35
Pirat:
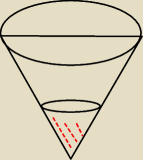
16 mar 19:38
Pirat: i że tam w tym czerwonym jest 1/8 tego całego stożka
16 mar 19:38
Metis: V=4πdm
3
Oblicz H...
16 mar 19:41
Pirat: no dobra wiem co mam zrobić ale jam masz V2 to masz dwie niewiadome nowe r2 i nowe H2.
16 mar 19:43
Pirat: Dlatego policzyłem z podobieństwa że H2 = 3r2/2
16 mar 19:43
Metis: Rozwiąże Ci to

16 mar 19:44
Metis:
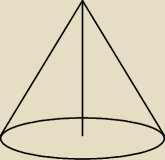
Liczę objetosc całego stożka:
| | 7 | | 7 | | 7 | |
V2= |
| V1⇔ |
| *4π= |
| πdm3 |
| | 8 | | 8 | | 2 | |
3−21/8=3/8 − szukana wysokosc
16 mar 19:51
Pirat: V2 − stożek o objętości 1/8 całego stożka.
Załóżmy że h= 3/8 , wtedy:
V2= 1/3 * r2 *3/8 *π = 1/2 π => r2 = 4 => r=2. Jak to jest możliwe że ma taki sam promień
jak stożek główny?
16 mar 20:20
Metis: A przepraszam pomyliłem się. Już poprawiam.
16 mar 20:24
Metis: Nie, przecież jest dobrze...
Ty źle rozumiesz.
Rozpatruje ten stożek z 19:38.
Jego objętość to różnica objętości całego stożka 4π i 7/8 objętości stożka , czyli
4π−3.5π=1/2π
Jego H = 3/8
Liczymy:
8π=18πr
2
r=2/3
Promień małego okregu, podstawy małego stożka.
16 mar 20:39
Metis: Ta musimy się nauczyć liczyć....
Poprawiam:
8πr
2*9=12π / π
72r
2=12
| | 1 | | √6 | |
r= |
| = |
| − szukany promień. |
| | √6 | | 6 | |
16 mar 20:48
Metis: Dobrze myślisz, ale źle liczyłeś

16 mar 20:49
Pirat: Czyli według Ciebie ten stożek z 19:38 zamalowany na czerwono ma r=2/3 , H=3/8 i jego V=1/2π?
16 mar 20:51
16 mar 20:53
Pirat: Przecież 3 skróci się na krzyż i wyjdzie 1/8πr2 = 1/2π => r=2
16 mar 20:53
Maciej Januszek : a mi to się wydaje, że to trzeba tak zrobić
3 trzeba podzielić przez osiem i koniec.
16 mar 20:54
Maciej Januszek : a przepraszam to jednak nie tak, ale prawie. Jeszcze trochę pomysle i zrobie ci to zadanko
16 mar 20:56
Metis: racja r=2 , nie mogę znaleźć błędu.
Tamte obliczenia mam błedne.
16 mar 20:59
Maciej Januszek : ale ja widze, Metisie otóż pomnożyłeś w poście z godziny 20.48 lewą strone równania błędnie
przez 24
16 mar 21:02
Metis: Nie chodzi mi o obliczenia. Piszę przeciez że są błędne . Nie widzę błędu w rozumowaniu.
16 mar 21:05
Metis: Napełniam cały stożek do 7/8 objętości , zostaje Nam 1/8 objętości.
Liczę do jakiej wysokości sięga 7/8 . Różnica całej wysokości i wyliczonej daje Nam wysokość
1/8 objętości.
16 mar 21:07
Maciej Januszek : zrozum, że musisz najpierw oblicz podzielić 3 przez 8, inaczej nic nie możesz
16 mar 21:08
Pirat:
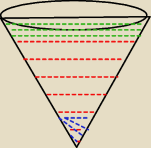
według twojego rozumowania wyznaczyłeś chyba 1/8 tego zielonego na górze a trzeba tutaj
wyznaczyć objętość tego niebieskiego. Czerwone to 7/8V
16 mar 21:10
Pirat: Bo wtedy H są całkowicie różne tak samo jak pola podstaw
16 mar 21:11
Maciej Januszek :
O, tak własnie wygląda rysunek poglądowy zrobiony u mnie w notatniku, trzeba to zadanie
obliczyć z twierdzenia elipsy konta w banku, cosinusa 30 stopni
16 mar 21:14
Mila:
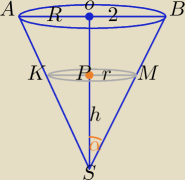
1)
SP=h
Stożek ABS∼Stożka KMS
V− objętość danego stożka
| | 1 | |
V'= |
| V objętość stożka utworzonego przez ciecz. |
| | 8 | |
Stosunek objętości figur podobnych jest równy sześcianowi skali podobieństwa.
| | 1 | |
Stożek KMS∼stożka ABS w skali k= |
| |
| | 2 | |
( jest dwa razy mniejszy od stożka danego)
[N==============]]
16 mar 23:09
Mila:
Jeżeli lubicie liczyć to tak:
|OS|=3
R=2
| | 1 | | 1 | |
V= |
| πR2*|OS|= |
| *π*22*3=4π |
| | 3 | | 3 | |
| | 1 | | 1 | | 4 | | 4π | |
V'= |
| π*r2*h= |
| π* |
| h2*h= |
| h3 |
| | 3 | | 3 | | 9 | | 27 | |
spr.
| | 1 | | 3 | | π | |
V'= |
| π*12* |
| = |
| zgodność. |
| | 3 | | 2 | | 2 | |
| | 3 | |
Należy wlać wodę do wysokości |
| dm , licząc od wierzchołka. |
| | 2 | |
(czyli do połowy stożka)
16 mar 23:09
Metis: Milu piękne dzięki

Powiedz co nie tak w rozumowaniu z 11:07

16 mar 23:10
Metis: *21:07
16 mar 23:10
Mila:
To jest stożek, tak byłoby w prostopadłościanie.
| 1 | |
| V od góry stożka to byłby bardzo mały słup cieczy. |
| 8 | |
Wypróbuj z kieliszkiem.
16 mar 23:25


 V=1/3Pp* H − w czym problem?
V=1/3Pp* H − w czym problem?


 Liczę objetosc całego stożka:
Liczę objetosc całego stożka:

 według twojego rozumowania wyznaczyłeś chyba 1/8 tego zielonego na górze a trzeba tutaj
wyznaczyć objętość tego niebieskiego. Czerwone to 7/8V
według twojego rozumowania wyznaczyłeś chyba 1/8 tego zielonego na górze a trzeba tutaj
wyznaczyć objętość tego niebieskiego. Czerwone to 7/8V
 O, tak własnie wygląda rysunek poglądowy zrobiony u mnie w notatniku, trzeba to zadanie
obliczyć z twierdzenia elipsy konta w banku, cosinusa 30 stopni
O, tak własnie wygląda rysunek poglądowy zrobiony u mnie w notatniku, trzeba to zadanie
obliczyć z twierdzenia elipsy konta w banku, cosinusa 30 stopni
 1)
SP=h
Stożek ABS∼Stożka KMS
V− objętość danego stożka
1)
SP=h
Stożek ABS∼Stożka KMS
V− objętość danego stożka
 Powiedz co nie tak w rozumowaniu z 11:07
Powiedz co nie tak w rozumowaniu z 11:07 