Geometria analityczna Geometria analityczna - liceum: zad.1 Punkty A(−3,1) B(2,0) i C(−1,−1) tworzą trójkąt ABC. a)Wyznacz współrzędne trójkąta A'B'C' będącego obrazem trójkąta ABC w przekształceniu, w którym punkt A' jest obrazem punktu A w symetrii osiowej względem prostej x=−1, punkt B' jest obrazem punktu B w translacji o wektor [−3,−1], natomiast C' jest obrazem punktu C w jednokładności o środku w punkcie B i skali −2 b) Oblicz o ile % pole trójkąta A'B'C' jest większe od pola trójkąta ABC.

Metis: Skąd to zadanie?

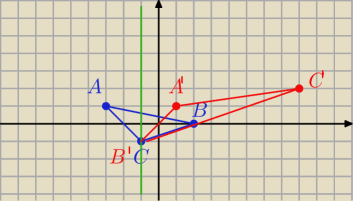
Janek191: A = ( − 3, 1) A ' = (x , 1)

− 3 + x
	= − 1 ⇒ x = 1
2

A ' = ( 1, 1) ======== B = ( 2, 0) więc B ' = ( 2, 0) = [ − 3, − 1] = ( 2 − 3, 0 − 1) = ( − 1 , − 1) = C B ' = ( − 1, − 1) ========== C = ( − 1, − 1) B = ( 2, 0) więc → → → BC ' = k BC = − 2 BC [ x − 2, y − 0 ] = − 2*[ − 1 − 2, − 1 − 0 ] = [ 6, 2 ] x − 2 = 6 y = 2 x = 8 y = 2 C ' = ( 8, 2) ========

Janek191: Miało być: B ' = ( 2, 0) + [ − 3, − 1 ] = ( − 1, − 1) = C