Geometria analityczna
Paulina E.C.H: Dany jest okrąg o równaniu (x−1)2+(y+4)2=36
a) Wyznacz równanie stycznych do tego okręgu i równoległych do osi układów współrzędnych
b) Wyznacz równanie stycznych do tego okręgu i równoległych do prostej o równaniu 2x+y−5=0
16 mar 12:50
Paulina E.C.H: równania*
16 mar 12:51
Jerzy:
To działaj...na kolejnego gotowca nie licz
16 mar 13:05
Paulina E.C.H: Nie liczę na gotowca, na sprawdzianie będę miała podobnego typu zadania i chcę się nauczyć
sposobu rozwiązania.
16 mar 13:09
Jerzy:
Gdzie leży środek i ile wynosi promień ?
16 mar 13:18
Paulina E.C.H: S=(1;−4)
r=6
16 mar 13:31
Janek191:
a)
Ile będzie tych stycznych ?
16 mar 13:32
Paulina E.C.H: 4
16 mar 13:36
Janek191:
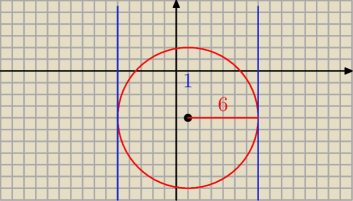
Styczne równoległe do osi OY :
x = 1 − 6 oraz x = 1 + 6
Odp. x = − 5 oraz x = 7
==================
16 mar 13:37
Jerzy:
Prostą rownoległą do osi OX przechodzàcą przez środek o ile trzeba przesunàć w górę i dół aby
była styczną ?
16 mar 13:37
Janek191:
b) analogicznie
16 mar 13:37
Paulina E.C.H: A do osi OY?
16 mar 13:38
Paulina E.C.H: OX*
16 mar 13:38
Jerzy:
Daj Janek dziewczynie pomyśleć...chce się nauczyć
16 mar 13:41
Paulina E.C.H: O tyle ile wynosi r
16 mar 13:45
Janek191:
To napisz odpowiedź
16 mar 13:47
Paulina E.C.H: Styczne równoległe do osi OX
y=−4−6 oraz y=−4+6
y=−10 oraz y=2
16 mar 13:52
Janek191:
ok
16 mar 13:55
Jerzy:
b) już nie będze analogicznie
jakie jest rownanie rownoleglych do danej prostej ?
16 mar 13:58
Janek191:
b) 2 x + y − 5 = 0
Napisz równanie prostej równoległej do danej odległej od S o r = 6.
2 x + y + C = 0
oraz wzór
| | I A x0 + B y0 + C I | |
r = |
| = 6 |
| | √A2 + B2 | |
S = (x
0, y
0) A = 2 B = 1
Oblicz C i napisz równania tych prostych.
16 mar 13:59
Jerzy:
Albo ...policz y , wstaw do równania okręgu i nałóż waruΔnek,aby równanie miało jedno
rozwiàzanie (Δ =0)
16 mar 14:03