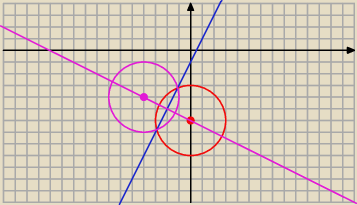
 O1 = ( 0, −6) r1 = 3
y = 2 x − 1
Prosta prostopadła do danej:
y = − 0,5 x + b
− 6 = −0,5*0 + b ⇒ b = − 6
y = −0,5 x − 6
Punkt wspólny tych prostych
2 x − 1 = − 0,5 x − 6 / *2
4 x − 2 = − x − 12
5 x = − 10
x = − 2
y = − 5
O2 jest symetryczny względem ( − 2, − 5 )
O2 = ( x, y)
O1 = ( 0, − 6)
O1 = ( 0, −6) r1 = 3
y = 2 x − 1
Prosta prostopadła do danej:
y = − 0,5 x + b
− 6 = −0,5*0 + b ⇒ b = − 6
y = −0,5 x − 6
Punkt wspólny tych prostych
2 x − 1 = − 0,5 x − 6 / *2
4 x − 2 = − x − 12
5 x = − 10
x = − 2
y = − 5
O2 jest symetryczny względem ( − 2, − 5 )
O2 = ( x, y)
O1 = ( 0, − 6)
| x + 0 | |
= − 2 ⇒ x = − 4 | |
| 2 |
| y − 6 | |
= − 5 ⇒ y − 6 = − 10 ⇒ y = − 4 | |
| 2 |