czworokąty i okręgi duo: zad.1 W równoległoboku, w którym jeden z boków jest dwa razy dłuższy od drugiego. kat ostry ma miarę 60 stopni a krótsza przekątna ma długość4√3. oblicz długości boków równoległoboku. zad.2 Dane są dwa okręgi współśrodkowe o różnych promieniach. Cięciwa większego okręgu jest styczna do mniejszego i ma długość 12 cm. Oblicz pole pierścienia kołowego utworzonego przez te okręgi. Bardzo proszę opomoc.

dero2005: d = 4√3 d² = (2a)² + a² − 2*2a*a*cos60^o a =

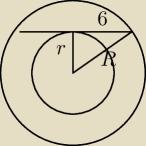
dero2005: R² − r² = 36 P = π(R² − r²) = 36π

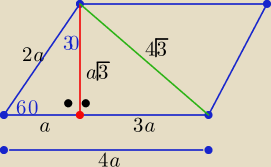
Eta: Bez tw. kosinusów ( na poziomie gimnazjum a>0 1/ 3a²+9a²=(4√3)² ⇒ 12a²=48 ⇒ a=2 to długości boków równoległoboku są równe : 8 i 4