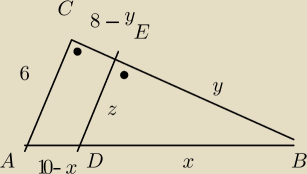
 w trójkącie ABC o bokach długości |AB|=10 , |BC|= 8 i |AC|= 6 poprowadzono prosta DE równoległa
do boku AC.
oblicz długości odcinków DB i EB, jesli prosta ED podzieliła:
b) trójkąt ABC na dwie figury o równych polach
Mój zamysł jest taki ,że
Tales
y(10−x) = x(8−y) +
PADCE = (6+z)... choć nie zastanawiam się czy nie warto by było podzielić ten czworokąt
na dwa mniejsze trójkąty tylko nie wiem czy było by to dobre rozwiązanie. wydaje mi się ,że
nie.
w trójkącie ABC o bokach długości |AB|=10 , |BC|= 8 i |AC|= 6 poprowadzono prosta DE równoległa
do boku AC.
oblicz długości odcinków DB i EB, jesli prosta ED podzieliła:
b) trójkąt ABC na dwie figury o równych polach
Mój zamysł jest taki ,że
Tales
y(10−x) = x(8−y) +
PADCE = (6+z)... choć nie zastanawiam się czy nie warto by było podzielić ten czworokąt
na dwa mniejsze trójkąty tylko nie wiem czy było by to dobre rozwiązanie. wydaje mi się ,że
nie.

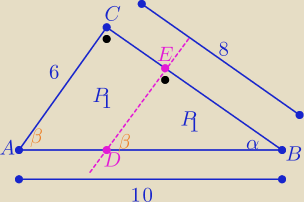 P(ABC)= 24 to P(BDE)=12
Trójkąty ABC i BDE są podobne z cechy (kkk) w skali k>0
P(ABC)= 24 to P(BDE)=12
Trójkąty ABC i BDE są podobne z cechy (kkk) w skali k>0
| P(ABC) | |
=k2 ⇒ k2=2 ⇒ k=√2 | |
| P(BDE) |
| 8 | 10 | |||
to |EB|= | = 4√2 i |DB|= | = 5√2 | ||
| √2 | √2 |





