Dany jest okrąg "0"o równaniu (x + 2)2 + (y − 6)2 = 4 . W drugiej „ćwiartce” układu
współrzędnych istnieją dwa okręgi o1, o2 styczne zewnętrznie do okręgu o0 i jednocześnie
styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów o1 oraz o2 .
Czyli So(−2,6) r=2
ro+2ro1(czerwony)=6
2+2ro1=6
r01=2
Rysunek trochę nagięty ale środek czerwonego do (−2,2)
Nie wiem gdzie lezy drugi okrąg 
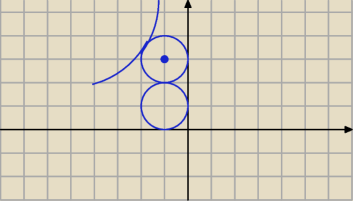Narysowałem jeden okrąg i drugi tylko częściowo bo jest dość duży.
S(−2,6) r = 2
S1(−2,2)
S2(−r2,r2) (bo styczny do osi)
|SS2| = 2 + r2
√(r2 − 2)2 + (r2 − 6)2 = 2 + r2 /2
r22 − 4r2 + 4 + r22 − 12r2 + 36 = 4 + 4r2 + r22
r22 − 20r2 + 36 = 0
Δ = 256
√Δ = 16
| 20 − 16 | ||
r2' = | = 2 (okrąg o1) | |
| 2 |
| 20 + 16 | ||
r2'' = | = 18 (okrąg o2) | |
| 2 |
