maturalne zadanko polo: W trójkącie równoramiennym ABC podstawa AB zawiera się w prostej k: x−y−15=0, zaś ramię BC zawiera się w prostej l: x+2y−12=0. Punkt P(2, −1) należy do ramienia AC. Oblicz wysokość tego trójkąta poprowadzoną na podstawe AB

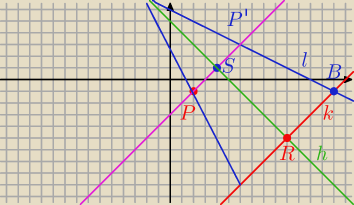
Janek191: k : y = x − 15 l : y = − 0,5 x + 6 x − 15 = −0,5 x + 6 / *2 2 x − 30 = − x + 12 3 x = 42 x = 14 y = 14 − 15 = − 1 B = ( 14, − 1) ========== Prosta równoległa do k przechodząca przez P = ( 2, −1) y = x + b − 1 = 2 + b ⇒ b = − 3 m : y = x − 3 ======= Punkt wspólny prostych m , l x − 3 = −0,5 x + 6 / *2 2 x − 6 = − x + 12 3 x = 18 x = 6 y = 3 P ' = ( 6, 3) S − środek odcinka P P ' S = ( 4, 1) Prosta prostopadła do k przechodząca przez S y = − x + b₁ 1 = − 4 + b₁ ⇒ b₁ = 5 h : y = − x + 5 ============ C − punkt wspólny prostych l, h − x + 5 = −0,5 x + 6 −0,5 x = 1 x = − 2 y = 7 C = ( − 2, 7) ======== Oblicz R oraz I CR I.

Henio: Mi wysokość wyszła 12√2