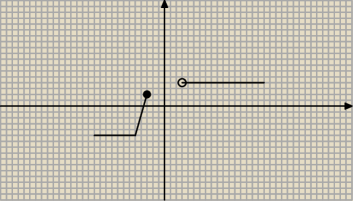
Monotoniczność funkcji lolek&bolek: Czy podana funkcja jest monotoniczna? Ja bym odpowiedział, że tak ponieważ jest niemalejąca, chociaż odpowiedź jest że nie jest monotoniczna.

kulas: Nie jest, ponieważ dla argumenty np 0 nie przyjmuje żadnej wartości

lolek&bolek: Nie za bardzo rozumiem, przecież definicja funkcji niemalejącej jest tutaj spełniona dla każdego x z dziedziny tej funkcji.

Bailar: Funkcja jest monotoniczna ale w swojej dziedzinie, nie mozesz mowic., ze dla całej funkcji ponieważ dla argumentyu0 nie przyjmuje wartosci

Bailar: Mógłbyś określić ja jako monotoniczna przedzialami

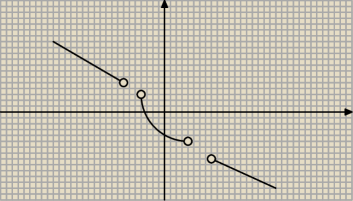
lolek&bolek: A taka jaka jest?

Janek191: Do 10.54 To zależy od definicji monotoniczności funkcji. Ta funkcja nie jest ściśle monotoniczna ( rosnąca), ale jest monotoniczna ( niemalejąca) w swojej dziedzinie.

lolek&bolek: @Janek191 też mi się tak wydaje. Wyjaśnienia z 0 jako argumentu nie kupuje dlatego że ten punkt nie jest w dziedzinie tej funkcji to po co go brać pod uwagę. Tam funkcji nie ma.

Jerzy: Funkcja monotoniczna nie musi być ciągła

kochanus_niepospolitus: Teoretycznie zarówno słaba wystarczy, że funkcja jest niemalejąca/nierosnąca (słabo monotoniczna), aby była ona monotoniczna ... jednak należy pamiętać, że niektórzy określenie monotoniczności funkcji stosują jedynie do przypadku funkcji rosnących/malejących (silna monotoniczność). Z tego też powodu, zapewne pierwszy przykład został uznany za funkcje, która nie jest monotoniczna.

kochanus_niepospolitus:

	1
Bailar ... a określić funkcje jako 'monotoniczna przedziałami' można by np. f(x) =
	|x|

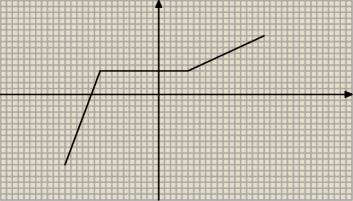
lolek&bolek: Poprzedni przykład w książce jest uznany za funkcje monotoniczną a jest on taki jak wyżej. Stąd moje wątpliwości.

Wyruchamwaszecorki: Tak dokładnie w tym wypadku miałabyś funkcje rosnąca w przedziale Od minus nieskończoności do 0 oraz malejącą od 0 do nieskończoności. O funkcji wykładnicza mowi sie ze jest monotoniczna w swoich przedziałach.

Wyruchamwaszecorki: Kretyn głupi nic nie wie o funkcji