Rozwiąż równanie wymierne infinite: Rozwiąż równanie wymierne: ^x+2_x+^x_x+2=2 Coś mi nie wychodzi, proszę o pomoc.

===: a cóż tu może nie wychodzić Pewnie lenistwo

infinite: wychodzi mi 4=0

Jerzy: Pokaż obliczenia

infinite: ((x+2)²+x²)/(x(x+2))=2 (x+2)²+x²=2x(x+2) x²+4x+4+x²=2x²+4x 4=0

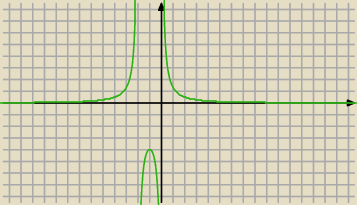
===: i to jest rozwiązanie ... wniosek oczywisty

Jerzy: Z wykresu wynika,że ma dwa rozwiązania...dla mnie jest sprzeczne

infinite: ok dziękuję

PW: Oczywiście że jest sprzeczne. Mamy do czynienia z równaniem typu

	1
a +		= 2,
	a

którego jedynym rozwiązaniem jest a = 1. U nas jest to niemożliwe, oznaczałoby bowiem

	x
		= 1,
	x+2

a to jest zdanie fałszywe dla dowolnych dopuszczalnych w tym zadaniu x.

===: a gdzie Ty Jerzy na tym wykresie widzisz rozwiązania

Jerzy: Prosta y = 2 tnie wykres

kochanus_niepospolitus: tyle, że === 'narysował' (a raczej nakazał narysować):

	x+2		x
f(x) =		+		−2
	x		x+2

a więc rozwiązania byłoby gdyby f(x) = 0

===: dokładnie