trygo klaraax: Udowodnij, że cos π/5*cos 3π/5= −1/4 Bardzo proszę o wyjaśnienie, bo gołe rozwiązanie już widziałam i nic nie rozumiem.. wiem że trzeba skorzystać z funkcji podwojonego kąta, ale kompletnie nie widzę co i jak...:(

PW: Nie z funkcji podwojonego kąta, ale z wzoru na sumę kosinusów:

	α+β		α−β
cosα + cosβ = 2cos		cos		.
	2		2

U nas

	α+β		3π
		=
	2		5

	α−β		π
		=		,
	2		5

co oznacza, że

	4π		2π
α =		i β =		,
	5		5

a więc mamy udowodnić równość

	1		4π		2π		1
		(cos		+ cos		) = −		.
	2		5		5		4

Jeżeli do pierwszego składnika zastosujemy wzór na kosinus podwojonego kąta, to dostaniemy

	2π		2π		1
2cos2		− 1 + cos		= −
	5		5		2

	2π		2π		1
(1) 2cos2		+ cos		−		= 0.
	5		5		2

Podstawmy

	2π
cos		= x.
	5

	1
2x2 + x −		= 0
	2

jest równaniem kwadratowym, którego jednym z rozwiązań jest, jak łatwo sprawdzić,

	−1+√5		2π
(2)		= cos		.
	4		5

Jeżeli mamy wiedzę wyrażoną wzorem (2), to wykazaliśmy tym samym prawdziwość zdania (1), które jest równoważne zadanej równości. Równość (2) można znaleźć w tablicach lub samemu udowodnić − zadanie brzmi: − Ile jest równy cos72°. Ale nie ucz się ode mnie, bo po pierwszej w nocy mam tendencję do gmatwania.

jc: cos 0 π/5 + cos 2 π/5 + cos 4 π/5 + cos 6 π/5 = 0. Kółko z 5 wektorami i wszystko jasne. cos 0 π/5 = 1 cos 2 π/5 = cos 6 π/5 cos 2 π/5 = cos 4 π/5 Dlatego cos 2 π/5 + cos 4 π/5 = −1/4

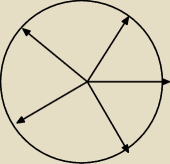
jc: jc: Suma 5 wektorów = 0 ⇒ suma rzutów na os poziomą = 0 ⇒ cos 0 π/5 + cos 2 π/5 + cos 4 π/5 + cos 6 π/5 + cos 8 π/5 = 0. cos 0 π/5 = 1, cos 2 π/5 = cos 8 π/5, cos 4 π/5 = cos 6 π/5 Dlatego cos 2 π/5 + cos 4 π/5 = −1/4

kochanus_niepospolitus:

	1		1
jc ... nie −		tylko −		powinieneś mieć
	4		2

jc: Oczywiście, że −1/2. Dziękuję! 1 + 2*suma = 0, suma = −1/2

jc: A to zadanie na śniadanie: oblicz (cos π/7 )*(cos 2π/7 )*(cos 3π/7 )

PW: jc, to rewelacyjne rozwiązanie, ale nie sądzę, żeby licealistka była przygotowana na takie rozumowanie. No chyba że odmłodziłem Klaręx Może się dziś odezwie.

ICSP:

	π		3π		π		2π
L = cos		* cos		= − cos		* cos		=
	5		5		5		5

	π   π   2π   2sin cos * cos   5   5   5
= −		=
	π   2sin   5

	2π   2π   2sin cos   5   5		4π   sin   5
= −		= −		=
	π   4sin   5		π   4sin   5

	1
= −		= P □
	4

PW: No, i to jest ładne rozwiązanie na "szkolnym" poziomie. I rzeczywiście zasadniczą rolę odgrywa wzór na sinus podwojonego kąta.

kochanus_niepospolitus: Bardzo ładne rozwiązanie ICSP, czego mi brakuje (a na pewno zarówno autorka, jak i reszta licealistów/studentów będzie chciała się zapytać) to objaśnienie (wiem że to 'idiotyczne', aby była konieczność tłumaczenia tego, ale cóż ... takie czasy):

	4π		π		π
sin		= sin (π −		) = sin
	5		5		5

	3π		2π		2π
sin		= sin (π −		) = sin
	5		5		5

PW: Czyżby o tym myślała Klaraax pisząc, że gołe rozwiązanie już widziała, ale nic nie rozumie? Miała rację, bo wzory redukcyjne to takie zdejmowanie ubranka

jc: Wzory redukcyjne widać na kółku. Propnuję ogólniejsze zadanie. Niech α = π/(2n+1). Znaleźć wartość iloczynu (cos α)(cos 2α)(cos 3α) . . . (cos nα)

ida: ICSP, moglbys to jakoś opisac? Powiedzieć z czego korzystasz?

kochanus (z komorki): Korzysta ze wzorow redukcyjnych (patrz moj wpis) oraz ze wzoru (dwukrotnie) na sinusa podwojonego kata